Section 1.11 answers to selected exercises
Subsection 1.11.1
Partial answer to exercise reported in Subsection 1.10.2. Listing 1.11.1. 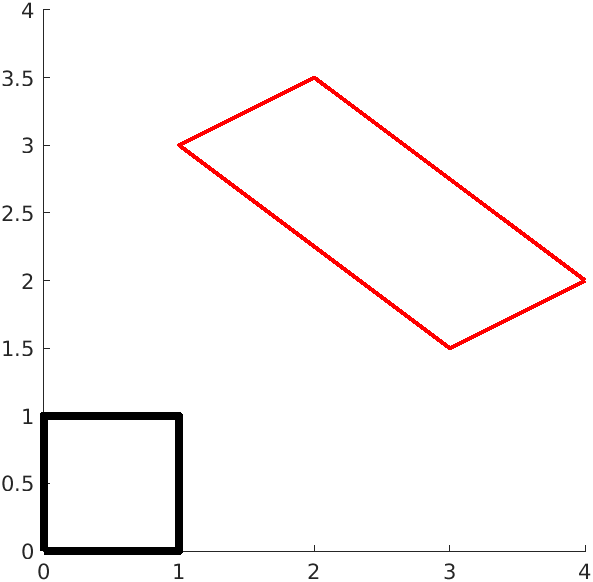
Figure 1.11.2.
$ % third question
T = @(X) [4-2*X(1)-X(2); 2+3/2*X(1)-X(2)/2];
Square_0 = [0 1 1 0 0; 0 0 1 1 0];
Square=[T(Square_0(:,1)) T(Square_0(:,2)) T(Square_0(:,3)) ...
T(Square_0(:,4)) T(Square_0(:,5))];
hold on
plot(Square_0(1,:), Square_0(2,:), 'k-', "LineWidth", 4)
plot(Square(1,:), Square(2,:), 'r-', "LineWidth", 2)
ylim([0 4])
pbaspect([1 1 1])

Subsection 1.11.2
Answer to exercise reported in Subsection 1.10.11. Listing 1.11.3.
$ X = sym('X', [3 1]);
u = sym('u', [3 1]);
u(1) = 3.5*10^(-3)*X(1) + 2.0*10^(-3)*X(2);
u(2) = 1.0*10^(-3)*X(1) - 0.5*10^(-3)*X(2);
u(3) = 0;
Du1 = gradient(u(1), X);
Du2 = gradient(u(2), X);
Du3 = gradient(u(3), X);
Du = [transpose(Du1); transpose(Du2); transpose(Du3)];
% first question
eps = (Du + transpose(Du))/2
% second question
[epsV,epsD] = eig(eps);
eps1 = eval(epsD(1,1));
eps2 = eval(epsD(2,2));
eps3 = eval(epsD(3,3));
% third question
I = diag([1 1 1]);
C = I + Du + transpose(Du) + transpose(Du)*Du;
[cV,cD] = eig(C);
lam1 = eval(sqrt(cD(1,1)));
lam2 = eval(sqrt(cD(2,2)));
lam3 = eval(sqrt(cD(3,3)));
% fourth question (compare eigenvalues)
% check that eps1 is almost equal to (lam1 - 1)
% check that eps2 is almost equal to (lam2 - 1)
% check that eps3 is almost equal to (lam3 - 1)
% fifth question (compare eigenvectors)
eval(epsV)
eval(cV)
