Section 1.3 deformation gradient
The transformation \(\vec{\chi}\) that was introduced to describe the motion of a body is completely generic therefore it is not necessarily linear. But we will see how this feature, linearity, still plays a fundamental role because, even if generic, \(\vec{\chi}\) can be described locally through its linearization. This idea is based on the notion of differential of a function.
In order to recall, in a simple way, the idea behind the linearization operations, this process is illustrated in the following figure for a real function depending on a single variable.
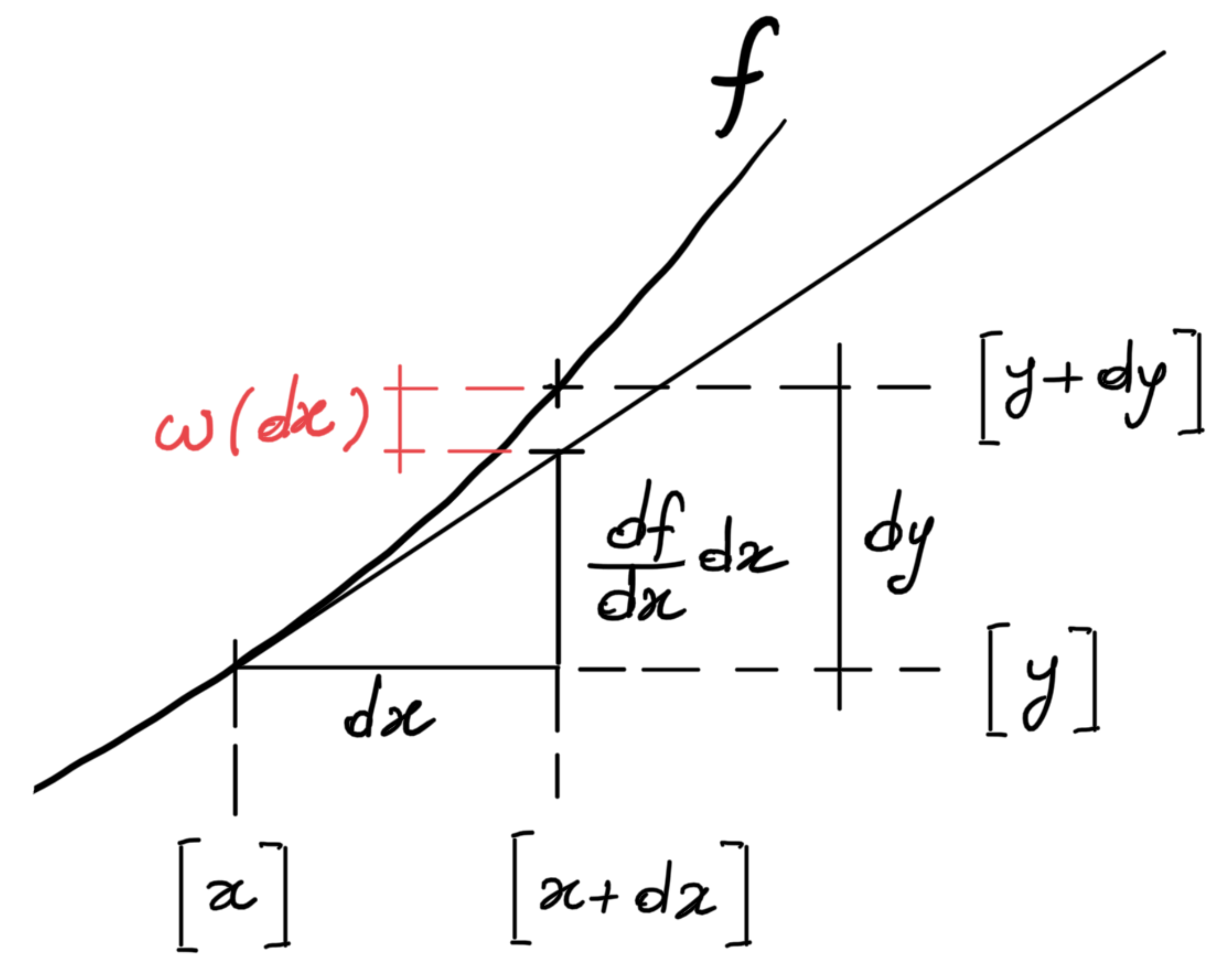
where \(\func{\omega}{dx}/dx \to 0\) if \(dx \to 0\text{,}\) then it is possible to state that
A rigorous generalization of the equation (1.3.1) would require additional instruments far beyond the introductory purposes of the present exposition. The final result is however given, result which provides the differential \(d\vec{x}\) relative to the current configuration as a function of the differential \(d\vec{X}\) relative to the reference configuration. For this purpose it si useful to write an expanded version of Equation (1.2.1)
The seeken differential can formulated as follows
These are a set of equations which can be expressed as multiplication between a matrix and a vector, i.e.
This result shows how the transition from \(d\vec{X}\) to \(d\vec{x}\) occurs through a linear transformation represented by the matrix \(\mat{F}\) which, for each point of the domain, contains all the information needed to characterize the deformation. \(\tens{F}\) is named as deformation gradient. On thsi basis the relationship between the differentials, \(d\vec{X}\) and \(d\vec{x}\text{,}\) can be expressed in compact form as
Relationship that can be specified more precisely as follows
where the dependence of \(\tens{F}\) on the point where the gradient is evaluated has been made explicit.
What is obtained for the transformation \(\vec{\chi} \) is also valid for its inverse \(\vec{\chi}^{-1}\text{,}\) therefore the following inverse relationship can be established between the differentials \(d\vec{X}\) and \(d\vec{x}\)
Typically the evaluation of the gradient of the inverse transformation does not pass through the explicit writing of \(\vec{\chi}^{- 1}\) but is done by calculating the inverse of \(\tens{F}\) for which invertibility must be ensured.
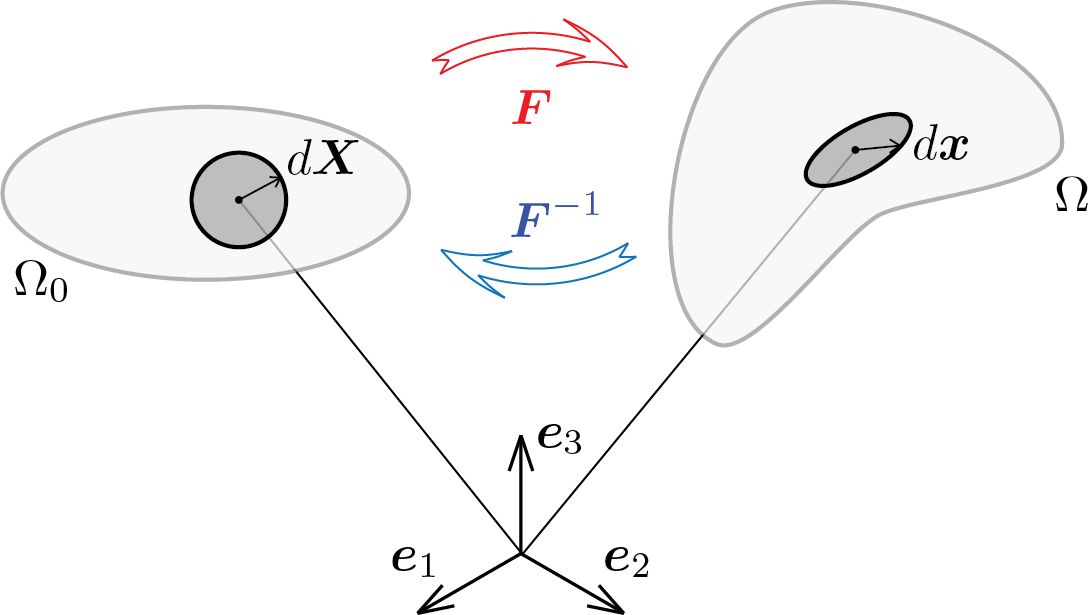
Remark 1.3.2.
It is instructive to compare this figure with the previous Figure 1.2.1 in order to keep enough separate the meaning of trasformation \(\vec{\chi} \) from its local representation through the deformation gradient.
evaluation of the deformation gradient (linear transformations).
In the case of Transformation 1 already discussed above, we make explicit the dependence of the individual components of \(\vec{x}\) on the components of \(\vec{X}\text{:}\)
From which the following partial derivatives are obtained
and therefore the deformation gradient
The fact that in this case we obtain a constant gradient equal to the matrix \(\mat{M_{\chi}}\) associated with the transformation is not accidental but depends on the linearity of the transformation under consideration: inevitably, its own linearization coincides with the given transformation. A similar result would also be obtained for the other linear transformations considered in the previous examples.
evaluation of the deformation gradient (nonlinear transformations).
In the case of nonlinear transformations it is not possible to identify a matrix associated with the transformation but, locally, the gradient of the transformation behaves like a linear transformation. Consider thus, for example, the transformation defined as
The calculation of the partial derivatives gives
allowing the evaluation of the deformation gradient
In order to visualize how the assigned transformation works let us consider, in the plane \((X_1, X_2)\text{,}\) three circumferences of radius \(0. \text{,}\) \(1.0\) and \(1.5\) and their configuratons obtained through the assigned nonlinear transformation. The MATLAB® instructions for the calculation and plotting of the circumferences in the reference configuration and in the current one are as reported below. N=60;
angle=linspace(0,2*pi,N);
radius=1.0;
c1X=radius*cos(angle);
c1Y=radius*sin(angle);
c1x=c1X.^3;
c1y=c1Y.^3;
radius=0.5;
c2X=radius*cos(angle);
c2Y=radius*sin(angle);
c2x=c2X.^3;
c2y=c2Y.^3;
radius=1.5;
c3X=radius*cos(angle);
c3Y=radius*sin(angle);
c3x=c3X.^3;
c3y=c3Y.^3;
hold on
% circumference (r=1), reference and deformed configurations
plot(c1X,c1Y,'b-')
plot(c1x,c1y,'b-')
% circumference (r=0.5), reference and deformed configurations
plot(c2X,c2Y,'r-')
plot(c2x,c2y,'r-')
% circumference (r=1.5), reference and deformed configurations
plot(c3X,c3Y,'m-')
plot(c3x,c3y,'m-')
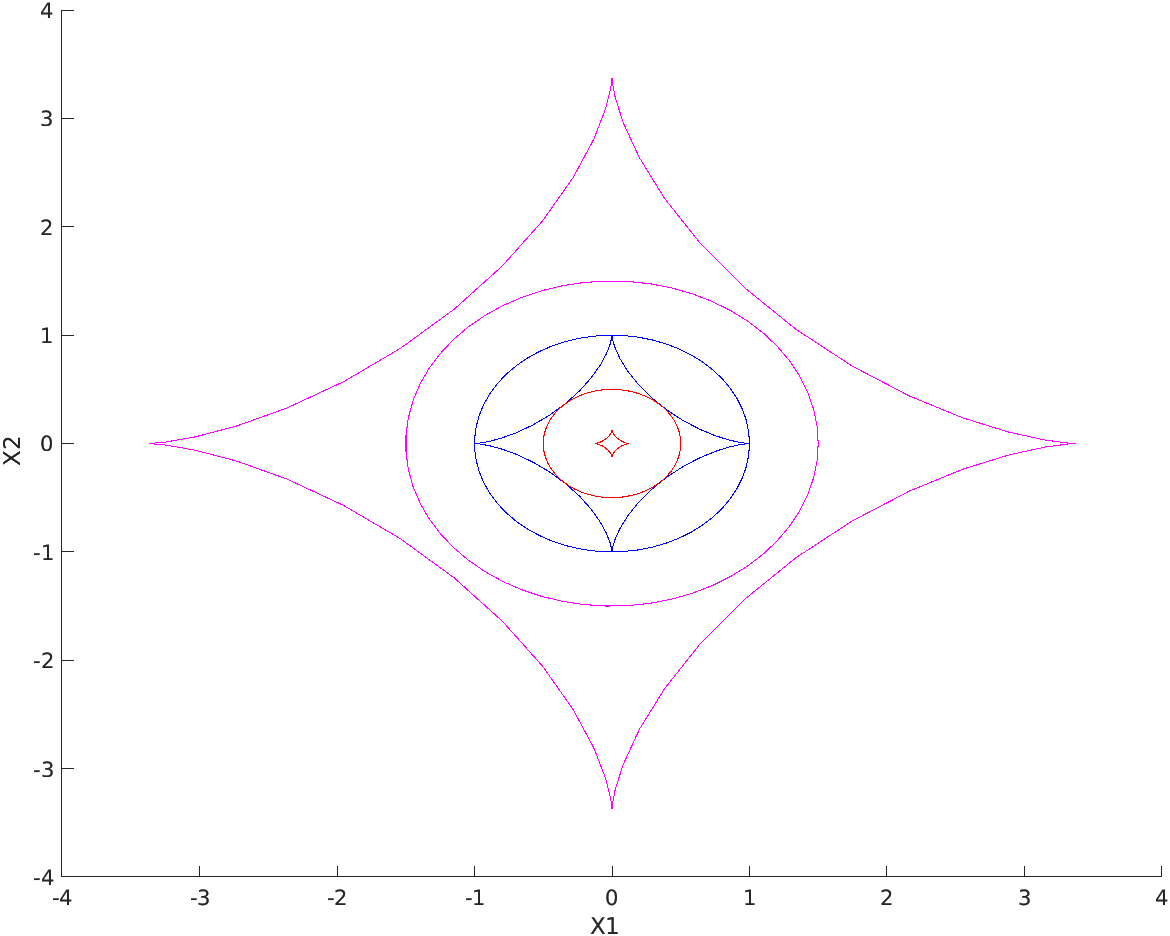
For exercise and to compare the nonlinear transformation examined with simpler linear transformations, it is suggested to perform the same calculations for the Transformations 2, 3 and 4 discussed in the previous sections.
Remark 1.3.5.
In the previous example, the cusps on the configurations obtained by applying the transformation are worth to be discussed. Can anything be said about them? The evaluation of the gradient on the points of the circle that are mapped onto the apexes of the cusps would allow to make a hypothesis on what happens in these points. Anyway further insight on this aspect will be given in the following section regarding the determinant of the deformation gradient.
Subsection 1.3.1 the notion of tensor
By introducing the deformation gradient \(\tens{F}\) we got acquainted with a category of mathematical objects which are called second order tensors or, simply, tensors, being superfluous to specify the order of the tensors that occur most often in solid mechanics. Certainly such an encounter can cause disorientation, especially if one is tempted to give a definition of the tensors in the most general form possible. Therefore, the most commonly used definition in Solid mechanics will be given, a definition which is also fairly obvious compared to what, regarding linear transformations, has been said so far.
Definition 1.3.6.
A second order tensor, which we will usually indicate in capital and bold letters (e.g. \(\tens{A}\text{,}\) \(\tens{B}\text{,}\) \(\tens{C}\text{,}\) \(\dots\)), is a linear transformation that associates to a generic vector \(\vec{u}\) another vector \(\vec{v}\text{.}\) This mapping is usually indicated as follows
and its linearity implies that
for all vectors \(\vec{u}\text{,}\) \(\vec{v}\) and all scalars \(\alpha\text{.}\)
