Solid Mechanics - the infinitesimal strain tensor

Section 1.9 the infinitesimal strain tensor

It often happens in applications that the norm of the displacement gradient is small. In these cases the contribution \(\transp{\tens{\nabla u}} \, \tens{\nabla u} \) appearing in the expressions of the tensor \(\tens{E}\) and tensor \(\tens{C}\) becomes negligible. Therefore the Green-Lagrange strain tensor will be coincident with the infinitesimal strain tensor \(\tens{\varepsilon}\text{,}\) i.e.

\begin{equation} \lim_{\|\tens{\nabla u}\| \rightarrow 0} \tens{E} = \tens{\varepsilon} = \frac{1}{2}\left(\tens{\nabla u} + \transp{\tens{\nabla u}}\right)\,,\label{infinitesima_1_eq}\tag{1.9.1} \end{equation}

while Cauchy tensor can be written as

\begin{equation} \lim_{\|\tens{\nabla u}\| \rightarrow 0} \tens{C} = \tens{I}+ \tens{\nabla u} + \transp{\tens{\nabla u}}\,.\label{infinitesima_2_eq}\tag{1.9.2} \end{equation}

Subsection 1.9.1 infinitesimal motions

Let us start by recalling the explicit expression of the components of the displacement \(\vec{u}\)

\begin{gather*} \func{u_1}{X_1, X_2, X_3}\,,\\ \func{u_2}{X_1, X_2, X_3}\,,\\ \func{u_3}{X_1, X_2, X_3}\,, \end{gather*}

and of its gradient \(\tens{\nabla u}\)

\begin{equation} \mat{\nabla u} = \left[\begin{array}{ccc} \regulardiff{u_1}{X_1} \amp \regulardiff{u_1}{X_2} \amp \regulardiff{u_1}{X_3}\\ \regulardiff{u_2}{X_1} \amp \regulardiff{u_2}{X_2} \amp \regulardiff{u_2}{X_3}\\ \regulardiff{u_3}{X_1} \amp \regulardiff{u_3}{X_2} \amp \regulardiff{u_3}{X_3} \end{array}\right]\,.\tag{1.9.3} \end{equation}

The following decomposition of \(\tens{\nabla u}\)

\begin{equation*} \tens{\nabla u} = \underbrace{\frac{1}{2}\left(\tens{\nabla u} + \transp{\tens{\nabla u}}\right)}_{\text{sym}\tens{\nabla u}} + \underbrace{\frac{1}{2}\left(\tens{\nabla u} - \transp{\tens{\nabla u}}\right)}_{\text{skew}\tens{\nabla u}}\,, \end{equation*}

true for all tensor, allows to insert in a more general framework the tensor of the infinitesimal strain previously introduced and the role played by \(\tens{\nabla u}\) in the description of the infinitesimal motions. By infinitesimal motions we will therefore mean the motions characterized by the condition \(\|\tens{\nabla u}\| \rightarrow 0\text{.}\)

The symmetric part, \(\text{sym}\tens{\nabla u}\text{,}\) whose matrix expression is
\begin{equation} \mat{\varepsilon} = \text{sym}\mat{\nabla u}= \left[\begin{array}{ccc} \regulardiff{u_1}{X_1} \amp \frac{1}{2}\left(\regulardiff{u_1}{X_2}+\regulardiff{u_2}{X_1}\right) \amp \frac{1}{2}\left(\regulardiff{u_1}{X_3}+\regulardiff{u_3}{X_1}\right)\\ \frac{1}{2}\left(\regulardiff{u_2}{X_1}+\regulardiff{u_1}{X_2}\right) \amp \regulardiff{u_2}{X_2} \amp \frac{1}{2}\left(\regulardiff{u_2}{X_3}+\regulardiff{u_3}{X_2}\right)\\ \frac{1}{2}\left(\regulardiff{u_3}{X_1}+\regulardiff{u_1}{X_3}\right) \amp \frac{1}{2}\left(\regulardiff{u_3}{X_2}+\regulardiff{u_2}{X_3}\right) \amp \regulardiff{u_3}{X_3} \end{array}\right]\,,\label{mat_symDu_eq}\tag{1.9.4} \end{equation}
gives the infinitesimal strain tensor \(\tens{\varepsilon}\) whose components are denoted as follows
\begin{equation} \mat{\varepsilon} = \left[\begin{array}{ccc} \varepsilon_{11} \amp \varepsilon_{12} \amp \varepsilon_{13}\\ \varepsilon_{21} \amp \varepsilon_{22} \amp \varepsilon_{23}\\ \varepsilon_{31} \amp \varepsilon_{32} \amp \varepsilon_{33} \end{array}\right]\,.\tag{1.9.5} \end{equation}
The skew part, \(\text{skew}\tens{\nabla u}\text{,}\) whose matrix expression is
\begin{equation} \text{skew}\mat{\nabla u}= \left[\begin{array}{ccc} 0 \amp \frac{1}{2}\left(\regulardiff{u_1}{X_2}-\regulardiff{u_2}{X_1}\right) \amp \frac{1}{2}\left(\regulardiff{u_1}{X_3}-\regulardiff{u_3}{X_1}\right)\\ \frac{1}{2}\left(\regulardiff{u_2}{X_1}-\regulardiff{u_1}{X_2}\right) \amp 0 \amp \frac{1}{2}\left(\regulardiff{u_2}{X_3}-\regulardiff{u_3}{X_2}\right)\\ \frac{1}{2}\left(\regulardiff{u_3}{X_1}-\regulardiff{u_1}{X_3}\right) \amp \frac{1}{2}\left(\regulardiff{u_3}{X_2}-\regulardiff{u_2}{X_3}\right) \amp 0 \end{array}\right]\,,\tag{1.9.6} \end{equation}
represents the infinitesimal rotation tensor.
For a generic infinitesimal motion we have
\begin{equation} \text{sym}\tens{\nabla u} \neq \tens{0}\,,\quad \text{skew}\tens{\nabla u} \neq \tens{0}.\tag{1.9.7} \end{equation}
For a rigid infinitesimal motion we have
\begin{equation} \text{sym}\tens{\nabla u} = \tens{0}\,,\quad \text{skew}\tens{\nabla u} \neq \tens{0}.\tag{1.9.8} \end{equation}

Insight 1.9.1. meaning of the components of the infinitesimal strain tensor.

In order to identify the meaning of the components of the tensor \(\tens{\varepsilon} \) it is better to start with the expression of tensor \(\tens{C}\) with respect to the gradient of the displacement, that is

\begin{equation*} \tens{C} = \tens{I}+ \tens{\nabla u} + \transp{\tens{\nabla u}} + \transp{\tens{\nabla u}}\,\tens{\nabla u}\,, \end{equation*}

from which, making the calculations, for example with the following MATLAB® instructions

syms u1_X1 u1_X2 u1_X3 u2_X1 u2_X2 u2_X3 u3_X1 u3_X2 u3_X3
Du = [u1_X1 u1_X2 u1_X3;u2_X1 u2_X2 u2_X3; u3_X1 u3_X2 u3_X3]
C = diag([1 1 1]) + Du + transpose(Du) + transpose(Du)*Du
C(1,1)
C(1,2)

Listing 1.9.2.

the expressions of a component on the main diagonal and one outside can be obtained, i.e.

\begin{align*} C_{11} \amp = \left( 1 + \frac{\partial u_1}{\partial X_1} \right)^2 + \left(\frac{\partial u_2}{\partial X_1}\right)^2 + \left(\frac{\partial u_3}{\partial X_1}\right)^2\,,\\ C_{12} \amp = \frac{\partial u_1}{\partial X_2} + \frac{\partial u_2}{\partial X_1} + \frac{\partial u_1}{\partial X_1}\frac{\partial u_1}{\partial X_2} + \frac{\partial u_2}{\partial X_1}\frac{\partial u_2}{\partial X_2} + \frac{\partial u_3}{\partial X_1}\frac{\partial u_3}{\partial X_2} \,. \end{align*}

For the diagonal component, using the (1.8.4) result obtained for the \(\tens{C}\) diagonal component, it is possible to write

\begin{equation*} \func{\lambda}{\vec{e}_1}^2 = \left( 1 + \underbrace{\frac{\partial u_1}{\partial X_1}}_{\varepsilon_{11}} \right)^2 + \underbrace{\left(\frac{\partial u_2}{\partial X_1}\right)^2 + \left(\frac{\partial u_3}{\partial X_1}\right)^2}_{\text{negligible in infinitesimal case}}\,. \end{equation*}

From which

\begin{equation} \varepsilon_{11} \approx \func{\lambda}{\vec{e}_1} - 1\,.\label{small_normal_strain_eq}\tag{1.9.9} \end{equation}

A similar result is valid for the other components of \(\tens{\varepsilon}\) belonging to the main diagonal.

For the off-diagonal component, by using (1.8.6), it can be obtained

\begin{equation*} \sin{\func{\gamma}{\vec{e}_1,\vec{e}_2}}\, \underbrace{\func{\lambda}{\vec{e}_1} \, \func{\lambda}{\vec{e}_2}}_{\approx 1} = \underbrace{\frac{\partial u_1}{\partial X_2} + \frac{\partial u_2}{\partial X_1}}_{2\,\varepsilon_{12}} + \underbrace{\frac{\partial u_1}{\partial X_1}\frac{\partial u_1}{\partial X_2} + \frac{\partial u_2}{\partial X_1}\frac{\partial u_2}{\partial X_2} + \frac{\partial u_3}{\partial X_1}\frac{\partial u_3}{\partial X_2}}_{\text{negligible in infinitesimal case}}\,, \end{equation*}

and then

\begin{equation} \varepsilon_{12} \approx \frac{1}{2}\, \sin{\func{\gamma}{\vec{e}_1,\vec{e}_2}} \approx \frac{1}{2}\, \func{\gamma}{\vec{e}_1,\vec{e}_2}\,.\label{small_shear_eq}\tag{1.9.10} \end{equation}

Insight 1.9.3. infinitesimal rotations.

To explain the denomination "infinitesimal rotation" that has been given to the skew part of the gradient of the displacement, it is convenient to discuss a transformation characterized only by a simple rotation. To this end, consider a rotation around the \(\vec{e}_3\) axis. The significant part of the transformation can be directly discussed in the plan as follows

\begin{align*} x_1 \amp = X_1\cos{\alpha} - X_2\sin{\alpha}\,,\\ x_2 \amp = X_1\sin{\alpha} + X_2\cos{\alpha}\,. \end{align*}

The displacement field is

\begin{align*} u_1 = x_1 - X_1 \amp = (X_1\cos{\alpha} - X_2\sin{\alpha}) - X_1\,,\\ u_2 = x_2 - X_2 \amp = (X_1\sin{\alpha} + X_2\cos{\alpha}) - X_2\,. \end{align*}

With this information it is possible to calculate the deformation gradient which, in the specific case, is composed only of the rotation

\begin{equation*} \tens{F} = \tens{R}\,, \end{equation*}

where, as already discussed before,

\begin{equation*} \mat{R} = \left[\begin{array}{cc} \cos{\alpha} \amp -\sin{\alpha} \\ \sin{\alpha} \amp \cos{\alpha} \end{array}\right]\,. \end{equation*}

Moreover

\begin{equation*} \tens{F} = \tens{I} + \tens{\nabla u}\,, \end{equation*}

and then

\begin{equation} \tens{R} = \tens{I} + \tens{\nabla u} = \tens{I} + \text{sym}\tens{\nabla u} + \text{skew}\tens{\nabla u}\,.\label{rotation_eq}\tag{1.9.11} \end{equation}

Result that highlights the decomposition of the gradient of the displacement with

\begin{equation*} \text{sym}\mat{\nabla u} = \left[\begin{array}{cc} \cos{\alpha} - 1 \amp 0 \\ 0 \amp \cos{\alpha} - 1 \end{array}\right]\,,\quad \text{skew}\mat{\nabla u} = \left[\begin{array}{cc} 0 \amp -\sin{\alpha} \\ \sin{\alpha} \amp 0 \end{array}\right]\,, \end{equation*}

decomposition that, for now, is generic because no reference to infinitesimal displacements has been introduced.

To assume infinitesimal displacements implies also very small values for the angle \(\alpha\text{,}\)\(\alpha \ll 1\text{,}\) i.e. \(\cos{\alpha}\approx 1\) and \(\sin{\alpha} \approx \alpha\text{.}\) From which

\begin{equation*} \text{sym}\mat{\nabla u} \approx \mat{0} \,,\quad \text{skew}\mat{\nabla u} \approx \left[\begin{array}{cc} 0 \amp -\alpha \\ \alpha \amp 0 \end{array}\right]\,. \end{equation*}

Therefore in the case of infinitesimal displacements expression (1.9.11) can be rewritten as follows

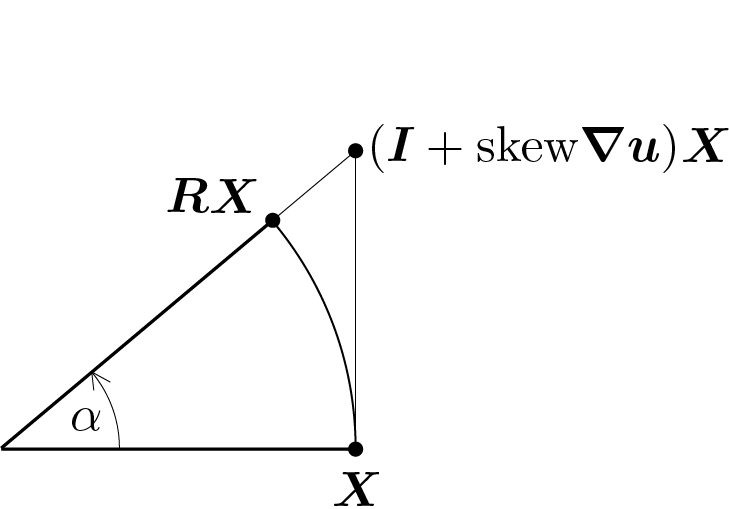
\begin{equation} \tens{R} \approx \tens{I} + \text{skew}\tens{\nabla u}\,.\label{rotation_infinitesima_eq}\tag{1.9.12} \end{equation}

Above in the figure the obtained result is emphasized showing the difference between the vector obtained by applying \(\tens{R}\)

\begin{equation*} \tens{R}\vec{X} \end{equation*}

and the vector obtained applying the approximation of \(\tens{R}\) given by \((\tens{I} + \text{skew}\tens{\nabla u})\)

\begin{equation*} (\tens{I} + \text{skew}\tens{\nabla u})\vec{X} = \vec{X} + \text{skew}\tens{\nabla u}\,\vec{X}\,. \end{equation*}

Insight 1.9.5.

Given a skew tensor \(\tens{W}\) characterized by the following matrix form

\begin{equation*} \mat{W} = \left[\begin{array}{ccc} 0 \amp W_{12} \amp W_{13}\\ -W_{12} \amp 0 \amp W_{23}\\ -W_{13} \amp -W_{23} \amp 0 \end{array}\right]\,, \end{equation*}

it easy to verify that to apply \(\tens{W}\) to a vector \(\vec{v}\)

\begin{equation*} \left[\begin{array}{ccc} 0 \amp W_{12} \amp W_{13}\\ -W_{12} \amp 0 \amp W_{23}\\ -W_{13} \amp -W_{23} \amp 0 \end{array}\right] \left[\begin{array}{c} v_1\\ v_2\\ v_3 \end{array}\right] = \left[\begin{array}{c} W_{12}v_2 + W_{13}v_3 \\ -W_{12}v_1 + W_{23}v_3\\ -W_{13}v_1 -W_{23}v_2 \end{array}\right] \end{equation*}

is equivalent to calculate the following vector or cross product

\begin{equation*} \left[\begin{array}{c} \omega_1\\ \omega_2\\ \omega_3 \end{array}\right] \times \left[\begin{array}{c} v_1\\ v_2\\ v_3 \end{array}\right] = \left[\begin{array}{c} \omega_2 v_3 - \omega_3 v_2\\ \omega_3 v_1 - \omega_1 v_3\\ \omega_1 v_2 - \omega_2 v_1 \end{array}\right] \end{equation*}

where the components of \(\vec{\omega}\) are related to the components of \(\tens{W}\) as follows

\begin{equation} \omega_{1} = -W_{23}\,,\quad \omega_{2} = W_{13}\,,\quad \omega_{3} = -W_{12}\,.\tag{1.9.13} \end{equation}

On the contrary, knowing \(\vec{\omega}\text{,}\) \(\tens{W}\) can be evaluated as follows

\begin{equation*} \mat{W} = \left[\begin{array}{ccc} 0 \amp -\omega_{3} \amp \omega_{2}\\ \omega_{3} \amp 0 \amp -\omega_{1}\\ -\omega_{2} \amp \omega_{1} \amp 0 \end{array}\right]\,. \end{equation*}

Eventually the following relationship can be stated

\begin{equation} \tens{W}\vec{v} = \vec{\omega} \times \vec{v}\,,\tag{1.9.14} \end{equation}

where \(\omega\) is the axial vector associated to the skew tensor \(\tens{W}\text{.}\) The adjective axial is used for the vector \(\omega\) because it represents the rotation axis of the infinitesimal rotation.