Skip to main content

Section 3.5 one-dimensional models: stretched beam

Subsection 3.5.1 premise

The solution of the elastic problem under completely generic conditions poses difficulties which are difficult to overcome. Only by making appropriate simplifications, such as for previous examples regarding prismatic solids (simple geometries) and under the action of loads of a precise type, is it possible to obtain an analytical solution of the assigned problem.

The previous considerations and the need to deal with engineering problems concerning solids which, from a geometric point of view, can be modeled through one-dimensional or two-dimensional descriptions, have led to the development of various structural models. These models allow to solve, with an acceptable degree of approximation, various problems that would not be easily tackled using both analytical and numerical tools.

In the following two beam models are presented. They are obtained through a one-dimensional reduction of the solutions found for prismatic solids simply stretched and simply bent, see Table 3.4.6. In particular, we will proceed by showing how it is possible to describe the significant component of the strain, the \(\varepsilon_{33} \text{,}\) referring only to the centerline of the beam, known as beam axis. The component \(\varepsilon_{33} \) is the significant one because it constitutes the only strain component that determines the value of the internal work of the prismatic solid, in fact in the two cases examined we have that

\begin{equation*} L_i = \int_{\body} \sigma_{33}\varepsilon_{33} \, dV\,, \end{equation*}

quantity that we will indicate by simply writing

\begin{equation} L_i = \int_{\body} \sigma\varepsilon \, dV\,,\label{beam_internal_work}\tag{3.5.1} \end{equation}

being clear which components we are referring to. So the main purpose is to obtain a description of the internal energy of the one-dimensional model equivalent to the internal energy of the 3D solution taken as a reference.

Furthermore, for the problems examined, the beam axis moves remaining in the plane identified by the axes \(X_3 \) and \(X_2 \) and for this reason the treatment can be carried out in the plane and then we will talk about 2D beam models  1 .

In the case of the stretched beam the one-dimensional solution should be valid also in a 3D context.

Subsection 3.5.2 the reference given by the beam axis

In the case of the prismatic solid that is simply stretched, the beam axis deforms as shown in the Figure, that is, it undergoes a simple elongation or shortening. The figure also highlights the notation that is currently used for this one-dimensional model.

Figure 3.5.1.

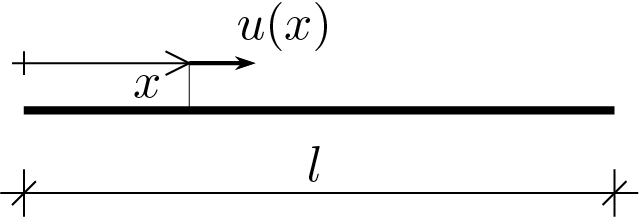
Using the beam axis as a reference, we can calculate the strain component \(\varepsilon_{33} \text{,}\) here simply referred to as \(\varepsilon \text{,}\) simply deriving the displacement variable along the axis

\begin{equation} \varepsilon = \frac{du}{dx}\,.\tag{3.5.2} \end{equation}

At the moment, as in the 3D reference solution, \(u \) is variable along the axis and the deformation \(\varepsilon \) is constant.

Subsection 3.5.3 internal work

It is possible now to rewrite the expression of the internal work (3.5.1) in a format that refers only to the beam axis, that is

\begin{align*} L_i \amp = \int_{\body} \sigma\varepsilon \, dV\\ \amp = \int_{l}\int_{A} \sigma\varepsilon \, dS \,dx\\ \amp = \int_{l}\int_{A} \sigma \, dS \varepsilon \,dx\\ \amp = \int_{l} N \varepsilon \,dx\,, \end{align*}

then

\begin{equation} L_i = \int_{l} N \varepsilon \,dx\,.\tag{3.5.3} \end{equation}

The introduced quantity

\begin{equation} N =\int_{A} \sigma \, dS\,,\label{trave_tesa_N}\tag{3.5.4} \end{equation}

is the static entity that in the one-dimensional reduction performs the internal work on strain. \(N\) is called axial force and is measured as a force, \(\left[\text{F}\right]\text{.}\)

Subsection 3.5.4 elastic constitutive law

The definition of the elastic law for the one-dimensional model is obtained by reworking Eq. (3.5.4) as follows

\begin{equation} N =\int_{A} \sigma \, dS = \int_{A} E\varepsilon \, dS = E\, \int_{A} dS \,\varepsilon = EA\,\varepsilon\,.\tag{3.5.5} \end{equation}

Relationship that highlights how the proportionality coefficient that defines the link between \(N \) and \(\varepsilon \) is given by the product between the Young's modulus of the material and the cross-section area of the beam.

Subsection 3.5.5 external work

Up to this point the one-dimensional reduction has remained strictly adherent to the 3D solution from which we started. If we continue on the same false line also for external loads you will get the following situation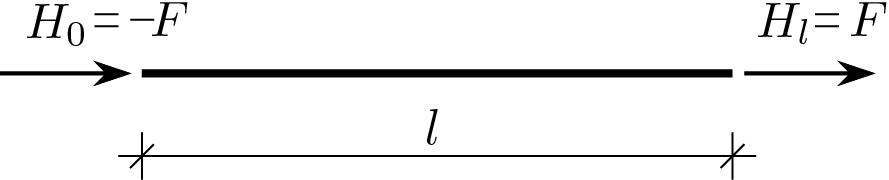

Figure 3.5.2.
that is, a beam simply subjected to two equal and opposite end forces.

With the definition of the external loads admissible for the beam model, the choice is made instead of extending the use of the model also to cases that in general are not included in the solution of the simply stretched prismatic solid. In particular, as the following Figure shows,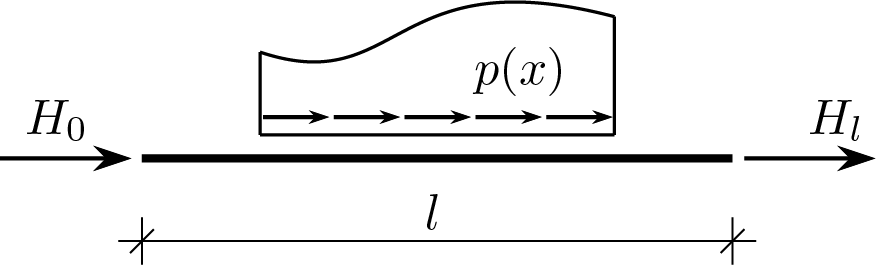

Figure 3.5.3.
we introduce the load per unit of length \(\func{p}{x} \text{,}\) a generic function dependent on the abscissa \(x \text{,}\) and the concetrated end forces, however expected, are generally different. The external work therefore assumes the following expression

\begin{equation} L_e = \int_{l} \func{p}{x}\,\func{u}{x}\, dx + H_{0} \,\func{u}{0} + H_{l} \,\func{u}{l}\,.\tag{3.5.6} \end{equation}

Furthermore, unlike the reference 3D solution, the choice of the admissible loads determines for \(\func{u}{x} \) a pattern which is no longer limited to linear variability alone. The normal stress and axial strain, constant in the reference solution, also become generic functions of the type \(\func{N}{x} \) and \(\func{\varepsilon}{x}\text{.}\)

Subsection 3.5.6 virtual work principle and equilibrium equations

At this point the definition of the model is practically complete. Only the definition of equilibrium equations, which can be obtained through the virtual work principle, is missing. The principle can be formulated as follows

\begin{equation} \int_{l} N \delta\varepsilon \,dx = \int_{l} p\,\delta u\, dx + H_{0} \,\func{\delta u}{0} + H_{l} \,\func{\delta u}{l}\,, \quad \forall\,\delta u \;\left(\delta\varepsilon = \frac{d\delta u}{d x}\right)\,.\tag{3.5.7} \end{equation}

The relationship just written, where we have neglected to make explicit the dependencies on the variable \(x \text{,}\) can be manipulated by carrying out the following steps

\begin{align*} \int_{l} N \delta\varepsilon \,dx \amp= \int_{l} p\,\delta u\, dx + H_{0} \,\func{\delta u}{0} + H_{l} \,\func{\delta u}{l}\\ \int_{l} N \frac{d\delta u}{d x} \,dx \amp= \int_{l} p\,\delta u\, dx + H_{0} \,\func{\delta u}{0} + H_{l} \,\func{\delta u}{l}\\ \left[N\,\delta u \right]_0^l - \int_{l} \frac{dN}{d x}\delta u \,dx \amp= \int_{l} p\,\delta u\, dx + H_{0} \,\func{\delta u}{0} + H_{l} \,\func{\delta u}{l}\\ \int_{l} \frac{dN}{d x}\delta u + \int_{l} p\,\delta u\, dx \,dx \amp= \left[N\,\delta u \right]_0^l - H_{0} \,\func{\delta u}{0} - H_{l} \,\func{\delta u}{l}\\ \int_{l} \left( \frac{dN}{d x} + p\right)\delta u\, dx \amp= \func{N}{l}\,\func{\delta u}{l} - \func{N}{0}\,\func{\delta u}{0} - H_{0} \,\func{\delta u}{0} - H_{l} \,\func{\delta u}{l}\\ \int_{l} \left( \frac{dN}{d x} + p\right)\delta u\, dx \amp= \left(\func{N}{l}- H_{l}\right)\func{\delta u}{l} - \left(\func{N}{0} + H_{0} \right)\func{\delta u}{0} \end{align*}

And then we get the following writing of the virtual work principle

\begin{equation} \int_{l} \left( \frac{dN}{d x} + p\right)\delta u\, dx = \left(\func{N}{l}- H_{l}\right)\func{\delta u}{l} - \left(\func{N}{0} + H_{0} \right)\func{\delta u}{0}\,,\quad \forall\,\delta u\,.\tag{3.5.8} \end{equation}

The satisfaction of this expression for any virtual displacement \(\delta u \) implies the satisfaction of the equation

\begin{equation} \frac{dN}{d x} + p = 0\,,\tag{3.5.9} \end{equation}

at each point of the beam axis and the fulfillment of the boundary conditions

\begin{align} \func{N}{0} \amp= -H_{0}\,,\tag{3.5.10}\\ \func{N}{l} \amp= H_{l}\,,\tag{3.5.11} \end{align}

on the ends of the beam axis.

Subsection 3.5.7 summary of the model

  • Loads
    \begin{equation*} \func{p}{x}\quad H_0 \quad H_l \end{equation*}
  • Unknowns
    \begin{equation*} \func{u}{x}\quad\func{\varepsilon}{x}\quad\func{N}{x} \end{equation*}
  • Internal work
    \begin{equation} L_i = \int_{l} N \varepsilon \,dx\,.\tag{3.5.12} \end{equation}
  • External work
    \begin{equation} L_e = \int_{l} \func{p}{x}\,\func{u}{x}\, dx + H_{0} \,\func{u}{0} + H_{l} \,\func{u}{l}\,.\tag{3.5.13} \end{equation}
  • Strain-displacement relationship
    \begin{equation} \varepsilon = \frac{du}{dx}\tag{3.5.14} \end{equation}
  • Elastic constitutive law
    \begin{equation} N = EA\,\varepsilon\tag{3.5.15} \end{equation}
  • Equilibrium equation
    \begin{equation} \frac{dN}{d x} + p = 0\tag{3.5.16} \end{equation}
  • Static boundary conditions
    \begin{align} \func{N}{0} \amp= -H_{0}\tag{3.5.17}\\ \func{N}{l} \amp= H_{l}\tag{3.5.18} \end{align}
  • Kinematic boundary conditions
    \begin{align} \func{u}{0} \amp= \bar{u}_{0}\tag{3.5.19}\\ \func{u}{l} \amp= \bar{u}_{l}\tag{3.5.20} \end{align}

As regards the boundary conditions, it is worth to be noted that on each end it is possible to assign either a static condition or a kinematic condition.

Equilibrium equation can be manipulated in order to obtain an expression in which the displacement \(\func{u}{x} \) appears as unknown. In particular by carrying out the following steps

\begin{align*} \frac{dN}{d x} + p \amp= 0\\ \frac{d}{d x}\left(EA\,\varepsilon\right) + p \amp= 0\\ \frac{d}{d x}\left(EA\,\frac{du}{dx}\right) + p \amp= 0 \end{align*}

the following result is obtained

\begin{equation} EA\,\frac{d^2u}{dx^2} + p = 0\,.\label{stretched_beam_navier}\tag{3.5.21} \end{equation}