Skip to main content

Section 1.2 transformations

Figure 1.2.1.

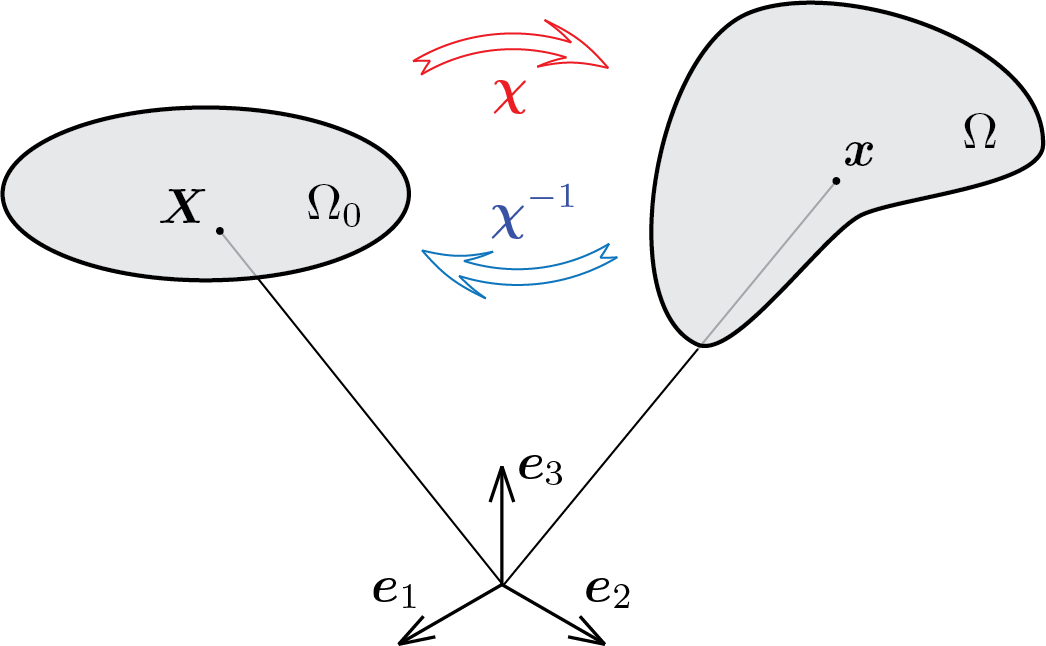
We call motion the trasformation

\begin{equation} \vec{x} = \func{\vec{\chi}}{\vec{X}}\,,\label{motion_eq}\tag{1.2.1} \end{equation}

valid \(\forall\vec{X} \in \body_0\text{.}\) \(\vec{\chi}\) is a vector function which, given a position \(\vec{X}\) relative to the reference configuration, provides the new position \(\vec{x}\) relative to the current configuration. The dependence between \(\vec{x}\) and \(\vec{X}\) is sometimes indicated shortly as follows

\begin{equation} \vec{x} = \func{\vec{x}}{\vec{X}}\,,\tag{1.2.2} \end{equation}

We assume \(\vec{\chi}\) sufficiently regular to allow derivation up to the desired order.

It is also assumed that the motion \(\vec{\chi} \) is uniquely invertible, i.e. it is possible to write

\begin{equation} \vec{X} = \func{\vec{\chi}^{-1}}{\vec{x}}\,,\tag{1.2.3} \end{equation}

or

\begin{equation} \vec{X} = \func{\vec{X}}{\vec{x}}\,,\tag{1.2.4} \end{equation}

where the symbol \(\vec{\chi}^{-1}\) indicates the inverse motion that associates the current position \(\vec{x}\) with the position \(\vec{X}\) in the reference configuration.

In general the motion \(\vec{\chi}\) of a body will change the position, orientation and shape of the body. A body capable of modifying its shape will therefore be called deformable.

some basic transformations.

Transformation 1 (90 degrees counterclockwise rotation)

\begin{equation*} \left[\begin{array}{c}x_1\\x_2\end{array}\right] = \func{\vec{\chi}}{\left[\begin{array}{c}X_1\\X_2\end{array}\right]} = \left[\begin{array}{c}-X_2\\X_1\end{array}\right] \end{equation*}

Instructions for the definition of a MATLAB® function associated with the assigned transformation and for its use. 

T1 = @(X) [-X(2); X(1)];

X = [1; 2];
T1(X)
Listing 1.2.2.

Transformation 2 (horizzontal extension)

\begin{equation*} \left[\begin{array}{c}x_1\\x_2\end{array}\right] = \func{\vec{\chi}}{\left[\begin{array}{c}X_1\\X_2\end{array}\right]} = \left[\begin{array}{c}2\,X_1\\X_2\end{array}\right] \end{equation*}

MATLAB® instructions. 

T2 = @(X) [2*X(1); X(2)];

X = [1; -1];
T2(X)
Listing 1.2.3.

Transformation 3 (vertical extension)

\begin{equation*} \left[\begin{array}{c}x_1\\x_2\end{array}\right] = \func{\vec{\chi}}{\left[\begin{array}{c}X_1\\X_2\end{array}\right]} = \left[\begin{array}{c}X_1\\1.5\,X_2\end{array}\right] \end{equation*}

MATLAB® instructions 

T3 = @(X) [X(1); 1.5*X(2)];

v = [4; 10];
T3(v)
Listing 1.2.4.

Transformation 4 (shear toward right)

\begin{equation*} \left[\begin{array}{c}x_1\\x_2\end{array}\right] = \func{\vec{\chi}}{\left[\begin{array}{c}X_1\\X_2\end{array}\right]} = \left[\begin{array}{c}X_1+X_2\\X_2\end{array}\right] \end{equation*}

MATLAB® instructions 

T4 = @(X) [X(1)+X(2); X(2)];

u = [10; -1];
T4(u)
Listing 1.2.5.

The previous examples belong to a very important class of transformations in solid mechanics: linear transformations.

As shown in previous video, in the case in which the transformation \(\vec{\chi}\) is linear its action on the vector \(\vec{X}\) can be transferred through the matrix \(\mat{M_{\chi}}\) defined as follows

\begin{equation} \mat{M_{\chi}} \equiv \left[\begin{array}{ccc} \func{\vec{\chi}}{\vec{e}_1} \amp \func{\vec{\chi}}{\vec{e}_2} \amp \func{\vec{\chi}}{\vec{e}_3} \end{array}\right]\,,\tag{1.2.5} \end{equation}

where \(\func{\vec{\chi}}{\vec{e}_1}\text{,}\) \(\func{\vec{\chi}}{\vec{e}_2}\) and \(\func{\vec{\chi}}{\vec{e}_3}\) are the vectors obtained by the application of the trasformation \(\vec{\chi}\) to the vectors forming the reference basis. Therefore the transformation of any vector \(\vec{X}\) can be obtained in an equivalent way by applying the matrix \(\mat{M_{\chi}}\text{:}\)

\begin{equation} \vec{x} = \func{\vec{\chi}}{\vec{X}} = \mat{M_{\chi}} \vec{X} \,.\tag{1.2.6} \end{equation}
evaluation of the matrix \(\mat{M_{\chi}}\).

In the case of the linear transformations already taken into consideration in the previous examples, it is easy to verify the following results.

Transformation 1

\begin{equation*} \mat{M_{\chi}} = \left[\begin{array}{cc} 0 \amp -1 \\ 1 \amp 0 \end{array}\right] \end{equation*}

Transformation 2

\begin{equation*} \mat{M_{\chi}} = \left[\begin{array}{cc} 2 \amp 0 \\ 0 \amp 1 \end{array}\right] \end{equation*}

Transformation 3

\begin{equation*} \mat{M_{\chi}} = \left[\begin{array}{cc} 1 \amp 0 \\ 0 \amp 1.5 \end{array}\right] \end{equation*}

Transformation 4

\begin{equation*} \mat{M_{\chi}} = \left[\begin{array}{cc} 1 \amp 1 \\ 0 \amp 1 \end{array}\right] \end{equation*}

MATLAB® instructions for the creation of the matrices associated with the given transformations. 

T1 = @(X) [-X(2); X(1)];
T2 = @(X) [2*X(1); X(2)];
T3 = @(X) [X(1); 1.5*X(2)];
T4 = @(X) [X(1)+X(2); X(2)];

M1 = [T1([1; 0]) T1([0; 1])]
M2 = [T2([1; 0]) T2([0; 1])]
M3 = [T3([1; 0]) T3([0; 1])]
M4 = [T4([1; 0]) T4([0; 1])]
Listing 1.2.6.

Remark 1.2.7.

It is important to underline again that it is possible to identify the matrix \(\mat{M_{\chi}}\) only in the case of linear transformation. Furthermore, the reverse is also true, i.e. the existence of a matrix \(\mat{M_{\chi}}\) usable to represent a transformation implies the linearity of the transformation.