l’ipotesi di continuità

Section 2.1 l’ipotesi di continuità

Alla base della meccanica del continuo vi è l’idea di studiare differenti fenomeni fisici senza una precisa conoscenza della micro-struttura interna della materia adottando il punto di vista, così detto, macroscopico. Ovvero si utilizzano una serie di quantità che rappresentano in forma media tutti i processi che avvengono a scala atomica o molecolare.

🔗

I sistemi macroscopici così definiti possono essere descritti in maniera efficace utilizzando l’approccio continuo che assume, per il corpo in esame, una distribuzione della materia continua nel spazio e nel tempo. Il corpo è sempre visto come un assemblaggio di singole particelle o punti da non confondere però con i sistemi di masse puntuali della meccanica Newtoniana o i sistemi di particelle della teoria atomica. Tipicamente il punto di un corpo continuo al suo interno nasconde una struttura interna (un accumulo di molecole o atomi ovvero una composizione etrogenea di vari costituenti) di dimensioni sufficientemente piccole se confrontate con la scala del problema in esame. Il comportamento del punto o particella è conseguenza del comportamento collettivo di tutto ciò che, al suo interno, costituisce il punto del continuo.

🔗

La continuità ha come conseguenze: la possibilità di effettuare una associazione uno-a-uno tra i punti del corpo e i punti della regione di spazio euclideo occupata dal corpo; la possibilità di suddividere un corpo in regioni di volume sempre più piccole e di ritrovare sempre le stesse caratteristiche fisiche al diminuire del volume.

🔗

L’analiticità delle funzioni utilizzate per descrivere il fenomeno fisico in esame consente di formulare le leggi fondamentali della meccanica in termini di equazioni differenziali.

🔗

L’approccio macroscopico alla base della meccanica del continuo è utilizzabile nello studio di solidi, fluidi e gas.

🔗

Subsection 2.1.1 descrizione geometrica dei corpi

L’ipotesi di continuità consente di identificare il corpo con un sottoinsieme aperto \(\body\) dello spazio euclideo. Per quanto già discusso nel capitolo dedicato alla cinematica, il corpo assumerà diverse configurazioni, nel seguito ci riferiremo ad una generica configurazione assunta dal corpo durante il suo moto. Su tale configurazione è possibile calcolare, ad esempio, il volume occupato dal corpo

\begin{equation} \func{v}{\body} = \int_{\body} dv \,.\tag{2.1.1} \end{equation}

🔗

Subsection 2.1.2 massa

La massa è una proprietà della materia che quantifica la sua resistenza all’accelerazione. In accordo con l’ipotesi di continuità si assume che la massa sia distribuita in maniera continua su tutto il corpo. In particolare si assume l’esistenza di un campo scalare \(\func{\rho}{\vec{x}} > 0\) denonimato densità di massa tale che

\begin{equation} \func{m}{\body} = \int_{\body} \func{\rho}{\vec{x}} dv \,.\tag{2.1.2} \end{equation}

Una definizione formale della massa può essere effettuata come segue. Sia \(\vec{x}\) un punto in \(\body\) e sia \(\func{\body_{\delta}}{\vec{x}}\) una famiglia di volumi tali che \(\func{v}{\func{\body_{\delta}}{\vec{x}}} \rightarrow 0\) se \(\delta \rightarrow 0\text{.}\) Allora

\begin{equation} \func{\rho}{\vec{x}} = \lim_{\delta \to 0} \frac{\func{m}{\func{\body_{\delta}}{\vec{x}}}}{\func{v}{\func{\body_{\delta}}{\vec{x}}}} \,.\tag{2.1.3} \end{equation}

Se tale limite esiste ed è positivo in ogni punto \(\vec{x}\) del corpo allora l’ipotesi di continuità è verificata. Inoltre il limite deve essere sempre lo stesso per qualsiasi famiglia di volumi \(\func{\body_{\delta}}{\vec{x}}\) avente la proprietà descritta.

🔗

Note 2.1.2.

L’idea moderna del limite di una funzione risale a Bolzano che, nel 1817, introdusse le basi della tecnica epsilon-delta per definire le funzioni continue. Tuttavia, il suo lavoro non era noto durante la sua vita. Il matematico francese Augustin-Louis Cauchy, nel suo libro della Cours d’analyse del 1821, ha discusso di quantità variabili, infinitesimi e limiti e ha definito la continuità di \(y = f(x)\) stabilendo che una variazione infinitesimale in \(x\) produce necessariamente una variazione infinitesimale in \(y\text{.}\)

🔗

Cauchy fu il primo a formulare la meccanica del continuo nel XIX secolo.

🔗

Subsection 2.1.3 forze

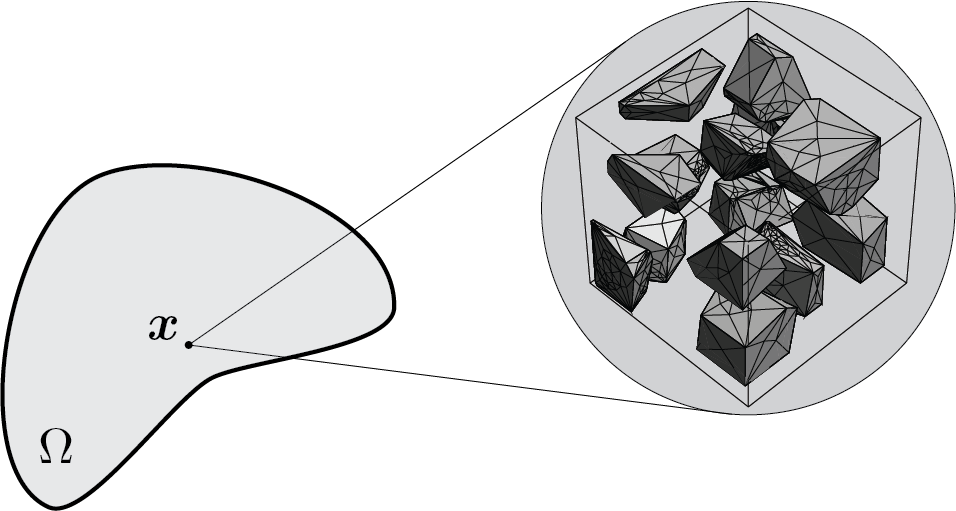
L’interazione meccanica fra parti di un corpo o di un corpo con l’ambiente circostante viene descritta mediante forze. Si considerano due tipi forze: forze di volume, che agiscono all’interno del corpo, e forze di superficie, che sono esercitate attraverso una superficie. Per l’ipotesi di continuità, come fatto per la massa, anche per le forze si postula l’esistenza di campi vettoriali che consentono di calcolare la risultante di tutte le forze agenti sul corpo

\begin{equation} \func{\vec{R}}{\body} = \int_{\body} \vec{b} \, dv + \int_{\partial\body} \vec{t} \, ds \,,\tag{2.1.4} \end{equation}

e il momento risultante (rispetto all’origine) delle forze agenti

\begin{equation} \func{\calvec{M}}{\body} = \int_{\body} \vec{x} \times \vec{b} \, dv + \int_{\partial\body} \vec{x} \times \vec{t} \, ds \,.\tag{2.1.5} \end{equation}

dove \(\partial\body\) denota il contorno di \(\body\) e quindi una superficie, \(\vec{b}\) e \(\vec{t}\) denotano due campi vettoriali che verranno meglio descritti nel seguito e che rappresentano, rispettivamente, una densità di forza di volume o, semplicemente, forza di volume e una densità di forza di superficie che verrà chiamata trazione.

🔗

Subsubsection 2.1.3.1 forza di volume

Le forze di volume non sorgono a causa di contatto fisico fra i corpi ma sono il risultato di un’azione a distanza, ad esempio la forza gravitazionale. Si assume quindi l’esistenza di una campo vettoriale \(\func{\vec{b}}{\vec{x}}\) funzione della posizione del punto \(\vec{x}\) appartenente a \(\body\text{.}\) In maniera analoga a quanto fatto per la densità di massa, è possibile dare una definizione formale di \(\func{\vec{b}}{\vec{x}}\text{:}\)

\begin{equation} \func{\vec{b}}{\vec{x}} = \lim_{\delta \to 0} \frac{\func{\vec{F}}{\func{\body_{\delta}}{\vec{x}}}}{\func{v}{\func{\body_{\delta}}{\vec{x}}}} \,,\tag{2.1.6} \end{equation}

dove \(\func{\vec{F}}{\func{\body_{\delta}}{\vec{x}}}\) è una forza a distanza agente sul volume \(\func{\body_{\delta}}{\vec{x}}\text{.}\)

🔗

Subsubsection 2.1.3.2 trazione

La trazione deriva dal contatto fisico tra corpi. Il contatto può avvenire attraverso il contorno \(\partial\body\) del corpo ed in questo caso si avrà una trazione esterna. Oppure, come discuteremo più diffusamente nel seguito, può avvenire attraverso una superficie ideale passante all’interno di un corpo, in questo caso si parlerà di trazione interna. Introduciamo quindi una definizione formale della trazione che ci consetirà di specificare la dipendenza di tale campo vettoriale.

🔗

Dato un punto \(\vec{x}\) del corpo posto all’interno o sulla frontiera di \(\body\text{,}\) e data una famiglia di superfici \(\func{\Gamma_{\delta}}{\vec{x}}\) passanti per tale punto tali che \(\func{a}{\func{\Gamma_{\delta}}{\vec{x}}}=\int_{\Gamma_\delta}ds \rightarrow 0\) se \(\delta \rightarrow 0\text{,}\) si assume l’esistenza di un campo vettoriale \(\func{\vec{t}}{\vec{x}, \Gamma_{\delta}}\) così definito

\begin{equation} \func{\vec{t}}{\vec{x},\Gamma_{\delta}} = \lim_{\delta \to 0} \frac{\func{\vec{F}}{\func{\Gamma_{\delta}}{\vec{x}}}}{\func{a}{\func{\Gamma_{\delta}}{\vec{x}}}} \,,\tag{2.1.7} \end{equation}

dove \(\func{\vec{F}}{\func{\Gamma_{\delta}}{\vec{x}}}\) è una forza di superficie agente sull’area \(\func{\Gamma_{\delta}}{\vec{x}}\text{.}\) \(\func{\vec{t}}{\vec{x}, \Gamma_{\delta}}\) prende il nome di vettore di trazione dipendente non solo da \(\vec{x}\) ma anche anche dalla famiglia di superfici passante per \(\vec{x}\text{.}\)

🔗

Un’opportuna definizione di tale dipendenza, elaborata da Cauchy, conduce alla nozione di tensore della tensione di Cauchy.

🔗

Prev Top Next