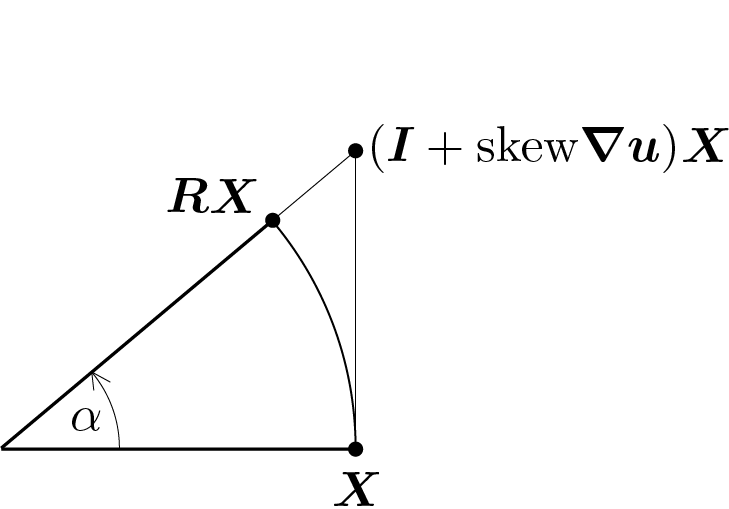tensore della deformazione infinitesima

Section 1.9 tensore della deformazione infinitesima

Accade spesso nelle applicazioni che l’entità del gradiente dello spostamento sia piccola. In questi casi il contributo dipendente da \(\transp{\tens{\nabla u}}\,\tens{\nabla u}\) e presente sia nel tensore \(\tens{E}\) sia nel tensore \(\tens{C}\) diventa trascurabile. Pertanto il tensore della deformazione di Green-Lagrange conciderà con il tensore della deformazione infinitesima \(\tens{\varepsilon}\)

\begin{equation} \lim_{\|\tens{\nabla u}\| \rightarrow 0} \tens{E} = \tens{\varepsilon} = \frac{1}{2}\left(\tens{\nabla u} + \transp{\tens{\nabla u}}\right)\,,\tag{1.9.1} \end{equation}

mentre il tensore di Cauchy assumerà la seguente espressione

\begin{equation} \lim_{\|\tens{\nabla u}\| \rightarrow 0} \tens{C} = \tens{I}+ \tens{\nabla u} + \transp{\tens{\nabla u}}\,.\tag{1.9.2} \end{equation}

🔗

Subsection 1.9.1 moti infinitesimi

Come premessa si ricordano le espressione esplicite del campo di spostamento \(\vec{u}\)

\begin{gather*} \func{u_1}{X_1, X_2, X_3}\,,\\ \func{u_2}{X_1, X_2, X_3}\,,\\ \func{u_3}{X_1, X_2, X_3}\,, \end{gather*}

e del relativo gradiente \(\tens{\nabla u}\)

\begin{equation} \mat{\nabla u} = \left[\begin{array}{ccc} \regulardiff{u_1}{X_1} \amp \regulardiff{u_1}{X_2} \amp \regulardiff{u_1}{X_3}\\ \regulardiff{u_2}{X_1} \amp \regulardiff{u_2}{X_2} \amp \regulardiff{u_2}{X_3}\\ \regulardiff{u_3}{X_1} \amp \regulardiff{u_3}{X_2} \amp \regulardiff{u_3}{X_3} \end{array}\right]\,.\tag{1.9.3} \end{equation}

La seguente decomposizione di \(\tens{\nabla u}\)

\begin{equation*} \tens{\nabla u} = \underbrace{\frac{1}{2}\left(\tens{\nabla u} + \transp{\tens{\nabla u}}\right)}_{\text{sym}\tens{\nabla u}} + \underbrace{\frac{1}{2}\left(\tens{\nabla u} - \transp{\tens{\nabla u}}\right)}_{\text{skew}\tens{\nabla u}}\,, \end{equation*}

in generale applicabile a tutti i tensori, consente di inserire in un quadro più generale il tensore della deformazione infinitesima prima introdotto ed il ruolo giocato da \(\tens{\nabla u}\) nella descrizione dei moti infinitesimi. Per moti infinitesimi intenderemo quindi i moti caratterizzati dalla condizione \(\|\tens{\nabla u}\| \rightarrow 0\text{.}\)

La parte simmetrica, \(\text{sym}\tens{\nabla u}\text{,}\) che in forma matriciale è esprimibile come
\begin{equation} \mat{\varepsilon} = \text{sym}\mat{\nabla u}= \left[\begin{array}{ccc} \regulardiff{u_1}{X_1} \amp \frac{1}{2}\left(\regulardiff{u_1}{X_2}+\regulardiff{u_2}{X_1}\right) \amp \frac{1}{2}\left(\regulardiff{u_1}{X_3}+\regulardiff{u_3}{X_1}\right)\\ \frac{1}{2}\left(\regulardiff{u_2}{X_1}+\regulardiff{u_1}{X_2}\right) \amp \regulardiff{u_2}{X_2} \amp \frac{1}{2}\left(\regulardiff{u_2}{X_3}+\regulardiff{u_3}{X_2}\right)\\ \frac{1}{2}\left(\regulardiff{u_3}{X_1}+\regulardiff{u_1}{X_3}\right) \amp \frac{1}{2}\left(\regulardiff{u_3}{X_2}+\regulardiff{u_2}{X_3}\right) \amp \regulardiff{u_3}{X_3} \end{array}\right]\,,\tag{1.9.4} \end{equation}
fornisce il tensore della deformazione infinitesima \(\tens{\varepsilon}\text{.}\) La notazione utilizzata per le singole componenti del tensore è
\begin{equation} \mat{\varepsilon} = \left[\begin{array}{ccc} \varepsilon_{11} \amp \varepsilon_{12} \amp \varepsilon_{13}\\ \varepsilon_{21} \amp \varepsilon_{22} \amp \varepsilon_{23}\\ \varepsilon_{31} \amp \varepsilon_{32} \amp \varepsilon_{33} \end{array}\right]\,.\tag{1.9.5} \end{equation}

🔗
La parte emisimmetrica, \(\text{skew}\tens{\nabla u}\text{,}\) che in forma matriciale è esprimibile come
\begin{equation} \text{skew}\mat{\nabla u}= \left[\begin{array}{ccc} 0 \amp \frac{1}{2}\left(\regulardiff{u_1}{X_2}-\regulardiff{u_2}{X_1}\right) \amp \frac{1}{2}\left(\regulardiff{u_1}{X_3}-\regulardiff{u_3}{X_1}\right)\\ \frac{1}{2}\left(\regulardiff{u_2}{X_1}-\regulardiff{u_1}{X_2}\right) \amp 0 \amp \frac{1}{2}\left(\regulardiff{u_2}{X_3}-\regulardiff{u_3}{X_2}\right)\\ \frac{1}{2}\left(\regulardiff{u_3}{X_1}-\regulardiff{u_1}{X_3}\right) \amp \frac{1}{2}\left(\regulardiff{u_3}{X_2}-\regulardiff{u_2}{X_3}\right) \amp 0 \end{array}\right]\,,\tag{1.9.6} \end{equation}
fornisce il tensore della rotazione infinitesima.

🔗
Nel caso di moto infinitesimo generico
\begin{equation} \text{sym}\tens{\nabla u} \neq \tens{0}\,,\quad \text{skew}\tens{\nabla u} \neq \tens{0}.\tag{1.9.7} \end{equation}

🔗
Nel caso di moto rigido infinitesimo
\begin{equation} \text{sym}\tens{\nabla u} = \tens{0}\,,\quad \text{skew}\tens{\nabla u} \neq \tens{0}.\tag{1.9.8} \end{equation}

🔗

🔗

Insight 1.9.1. interpretazione delle componenti del tensore della deformazione infinitesima.

Al fine di individuare il significato delle componenti del tensore \(\tens{\varepsilon}\) conviene richiamare l’espressione del tensore \(\tens{C}\) rispetto al gradiente delo spostamento, ovvero

\begin{equation*} \tens{C} = \tens{I}+ \tens{\nabla u} + \transp{\tens{\nabla u}} + \transp{\tens{\nabla u}}\,\tens{\nabla u}\,, \end{equation*}

da cui, effettuando i calcoli, ad esempio con le seguenti istruzioni MATLAB®

🔗

Listing 1.9.2.

🔗

$ syms u1_X1 u1_X2 u1_X3 u2_X1 u2_X2 u2_X3 u3_X1 u3_X2 u3_X3
Du = [u1_X1 u1_X2 u1_X3;u2_X1 u2_X2 u2_X3; u3_X1 u3_X2 u3_X3]
C = diag([1 1 1]) + Du + transpose(Du) + transpose(Du)*Du
C(1,1)
C(1,2)

si possono ricavare le espressioni di una componente sulla diagonale ed una fuori dalla diagonale

\begin{align*} C_{11} \amp = \left( 1 + \frac{\partial u_1}{\partial X_1} \right)^2 + \left(\frac{\partial u_2}{\partial X_1}\right)^2 + \left(\frac{\partial u_3}{\partial X_1}\right)^2\,,\\ C_{12} \amp = \frac{\partial u_1}{\partial X_2} + \frac{\partial u_2}{\partial X_1} + \frac{\partial u_1}{\partial X_1}\frac{\partial u_1}{\partial X_2} + \frac{\partial u_2}{\partial X_1}\frac{\partial u_2}{\partial X_2} + \frac{\partial u_3}{\partial X_1}\frac{\partial u_3}{\partial X_2} \,. \end{align*}

Per la componente sulla diagonale, utilizzando il risultato (1.8.4) ottenuto per la componente sulla diagonale di \(\tens{C}\text{,}\) si può scrivere

\begin{equation*} \func{\lambda}{\vec{e}_1}^2 = \left( 1 + \underbrace{\frac{\partial u_1}{\partial X_1}}_{\varepsilon_{11}} \right)^2 + \underbrace{\left(\frac{\partial u_2}{\partial X_1}\right)^2 + \left(\frac{\partial u_3}{\partial X_1}\right)^2}_{\text{trascurabili nel caso infinitesimo}}\,. \end{equation*}

Da cui si ricava

\begin{equation} \varepsilon_{11} \approx \func{\lambda}{\vec{e}_1} - 1\,.\tag{1.9.9} \end{equation}

Analogo risultato vale per le altre componenti di \(\tens{\varepsilon}\) sulla diagonale.

🔗

Per la componente fuori dalla diagonale, utilizzando il risultato (1.8.6), si ha

\begin{equation*} \sin{\func{\gamma}{\vec{e}_1,\vec{e}_2}}\, \underbrace{\func{\lambda}{\vec{e}_1} \, \func{\lambda}{\vec{e}_2}}_{\approx 1} = \underbrace{\frac{\partial u_1}{\partial X_2} + \frac{\partial u_2}{\partial X_1}}_{2\,\varepsilon_{12}} + \underbrace{\frac{\partial u_1}{\partial X_1}\frac{\partial u_1}{\partial X_2} + \frac{\partial u_2}{\partial X_1}\frac{\partial u_2}{\partial X_2} + \frac{\partial u_3}{\partial X_1}\frac{\partial u_3}{\partial X_2}}_{\text{trascurabili nel caso infinitesimo}}\,, \end{equation*}

e quindi

\begin{equation} \varepsilon_{12} \approx \frac{1}{2}\, \sin{\func{\gamma}{\vec{e}_1,\vec{e}_2}} \approx \frac{1}{2}\, \func{\gamma}{\vec{e}_1,\vec{e}_2}\,.\tag{1.9.10} \end{equation}

🔗

Insight 1.9.3. rotazioni infinitesime.

Per spiegare la denominazione "rotazione infinitesima" che è stata data alla parte emisimmetrica del gradiente dello spostamento conviene discutere in concreto una trasformazione caratterizzata solo da una semplice rotazione. A tal fine si consideri una rotazione intorno all’asse \(\vec{e}_3\text{.}\) La parte significativa della trasformazione può essere discussa direttamente nel piano con

\begin{align*} x_1 \amp = X_1\cos{\alpha} - X_2\sin{\alpha}\,,\\ x_2 \amp = X_1\sin{\alpha} + X_2\cos{\alpha}\,. \end{align*}

Il campo di spostamento associato è

\begin{align*} u_1 = x_1 - X_1 \amp = (X_1\cos{\alpha} - X_2\sin{\alpha}) - X_1\,,\\ u_2 = x_2 - X_2 \amp = (X_1\sin{\alpha} + X_2\cos{\alpha}) - X_2\,. \end{align*}

Con tali dati è possibile calcolare il gradiente della trasformazione che, nel caso specifico, è composto solo dalla rotazione

\begin{equation*} \tens{F} = \tens{R}\,, \end{equation*}

dove, come già discusso nelle sezioni precedenti,

\begin{equation*} \mat{R} = \left[\begin{array}{cc} \cos{\alpha} \amp -\sin{\alpha} \\ \sin{\alpha} \amp \cos{\alpha} \end{array}\right]\,. \end{equation*}

Inoltre

\begin{equation*} \tens{F} = \tens{I} + \tens{\nabla u}\,, \end{equation*}

e quindi

\begin{equation} \tens{R} = \tens{I} + \tens{\nabla u} = \tens{I} + \text{sym}\tens{\nabla u} + \text{skew}\tens{\nabla u}\,.\tag{1.9.11} \end{equation}

Risultato che evidenzia la decomposizione del gradiente dello spostamento con

\begin{equation*} \text{sym}\mat{\nabla u} = \left[\begin{array}{cc} \cos{\alpha} - 1 \amp 0 \\ 0 \amp \cos{\alpha} - 1 \end{array}\right]\,,\quad \text{skew}\mat{\nabla u} = \left[\begin{array}{cc} 0 \amp -\sin{\alpha} \\ \sin{\alpha} \amp 0 \end{array}\right]\,, \end{equation*}

ma ancora del tutto generico e che non fa riferimento agli spostamenti infinitesimi.

🔗

Ipotizzare spostamenti infinitesimi equivale ad assumere valori dell’angolo \(\alpha\) molto piccoli, \(\alpha \ll 1\text{,}\) ovvero \(\cos{\alpha}\approx 1\) e \(\sin{\alpha} \approx \alpha\text{.}\) Da cui deriva

\begin{equation*} \text{sym}\mat{\nabla u} \approx \mat{0} \,,\quad \text{skew}\mat{\nabla u} \approx \left[\begin{array}{cc} 0 \amp -\alpha \\ \alpha \amp 0 \end{array}\right]\,. \end{equation*}

Pertanto nel caso di spostamenti infinitesi la relazione (1.9.11) può essere riscritta come segue

\begin{equation} \tens{R} \approx \tens{I} + \text{skew}\tens{\nabla u}\,.\tag{1.9.12} \end{equation}

🔗

La Figura illustra graficamente il risultato ottenuto mostrando anche in che relazione stanno il vettore ottenuto applicando \(\tens{R}\)

\begin{equation*} \tens{R}\vec{X} \end{equation*}

e il vettore ottenuto applicando l’approssimazione di \(\tens{R}\) data da \((\tens{I} + \text{skew}\tens{\nabla u})\)

\begin{equation*} (\tens{I} + \text{skew}\tens{\nabla u})\vec{X} = \vec{X} + \text{skew}\tens{\nabla u}\,\vec{X}\,. \end{equation*}

🔗

Insight 1.9.5.

Dato un tensore \(\tens{W}\) emisimmetrico, la cui forma matriciale ad esso associata per definizione sarà

\begin{equation*} \mat{W} = \left[\begin{array}{ccc} 0 \amp W_{12} \amp W_{13}\\ -W_{12} \amp 0 \amp W_{23}\\ -W_{13} \amp -W_{23} \amp 0 \end{array}\right]\,, \end{equation*}

si può verificare come la sua applicazione ad un vettore \(\vec{v}\)

\begin{equation*} \left[\begin{array}{ccc} 0 \amp W_{12} \amp W_{13}\\ -W_{12} \amp 0 \amp W_{23}\\ -W_{13} \amp -W_{23} \amp 0 \end{array}\right] \left[\begin{array}{c} v_1\\ v_2\\ v_3 \end{array}\right] = \left[\begin{array}{c} W_{12}v_2 + W_{13}v_3 \\ -W_{12}v_1 + W_{23}v_3\\ -W_{13}v_1 -W_{23}v_2 \end{array}\right] \end{equation*}

equivalga a calcolare il seguente prodotto vettoriale

\begin{equation*} \left[\begin{array}{c} \omega_1\\ \omega_2\\ \omega_3 \end{array}\right] \times \left[\begin{array}{c} v_1\\ v_2\\ v_3 \end{array}\right] = \left[\begin{array}{c} \omega_2 v_3 - \omega_3 v_2\\ \omega_3 v_1 - \omega_1 v_3\\ \omega_1 v_2 - \omega_2 v_1 \end{array}\right] \end{equation*}

dove le componenti di \(\vec{\omega}\) sono messe in corrispondenza con le componenti di \(\tens{W}\) nel modo seguente

\begin{equation} \omega_{1} = -W_{23}\,,\quad \omega_{2} = W_{13}\,,\quad \omega_{3} = -W_{12}\,.\tag{1.9.13} \end{equation}

Quindi, noto \(\vec{\omega}\text{,}\) \(\tens{W}\) può essere espresso come segue

\begin{equation*} \mat{W} = \left[\begin{array}{ccc} 0 \amp -\omega_{3} \amp \omega_{2}\\ \omega_{3} \amp 0 \amp -\omega_{1}\\ -\omega_{2} \amp \omega_{1} \amp 0 \end{array}\right]\,. \end{equation*}

🔗

Pertanto si ha

\begin{equation} \tens{W}\vec{v} = \vec{\omega} \times \vec{v}\,,\tag{1.9.14} \end{equation}

e \(\omega\) è il vettore assiale associato al tensore emisimmetrico \(\tens{W}\text{.}\) L’aggettivo assiale deriva dal fatto che \(\omega\) individua l’asse di una rotazione intorno al quale si effettua la rotazione infinitesima.

🔗

Prev Top Next