Paragrafo 1.6 decomposizione polare
La possibilità che una data trasformazione lineare possa essere il risultato della composizione di più trasformazioni lineari e la considerazione fisica che il moto di un corpo si compone di trasformazioni elementari come la rotazione e la deformazione pura, portano al seguente risultato fondamentale e formalizzabile in termini di teorema.
teorema di decomposizione polare.
Dato il gradiente della deformazione \(\func{\tens{F}}{\vec{X}}\text{,}\) in ogni punto del corpo soggetto al moto esiste un'unica decomposizione polare definita come segue
\(\tens{R}\) è il tensore di rotazione, quindi un tensore ortogonale proprio, che soddisfa la relazione
\(\tens{U}\) e \(\tens{V}\) sono, rispettivamente, il tensore destro di deformazione e il tensore sinistro di deformazione. Tali tensori sono unici, definiti positivi e simmetrici. Il fatto che \(\tens{U}\) e \(\tens{V}\) siano definiti positivi impone che per qualsiasi vettore \(\vec{v} \neq \vec0\) sia soddisfatta la proprietà
mentre la simmetria impone che
Osservazione 1.6.1.
Applicando la decomposizione polare destra alla relazione (1.3.9) si ottiene
che evidenzia come il vettore \(d\vec{X}\) venga prima deformato e poi ruotato. Applicando invece la decomposizione polare sinistra si ottiene
da interpretare come sequenza di deformazione di \(d\vec{X}\) seguita da una rotazione. Quanto detto viene illustrato dalla seguente figura. 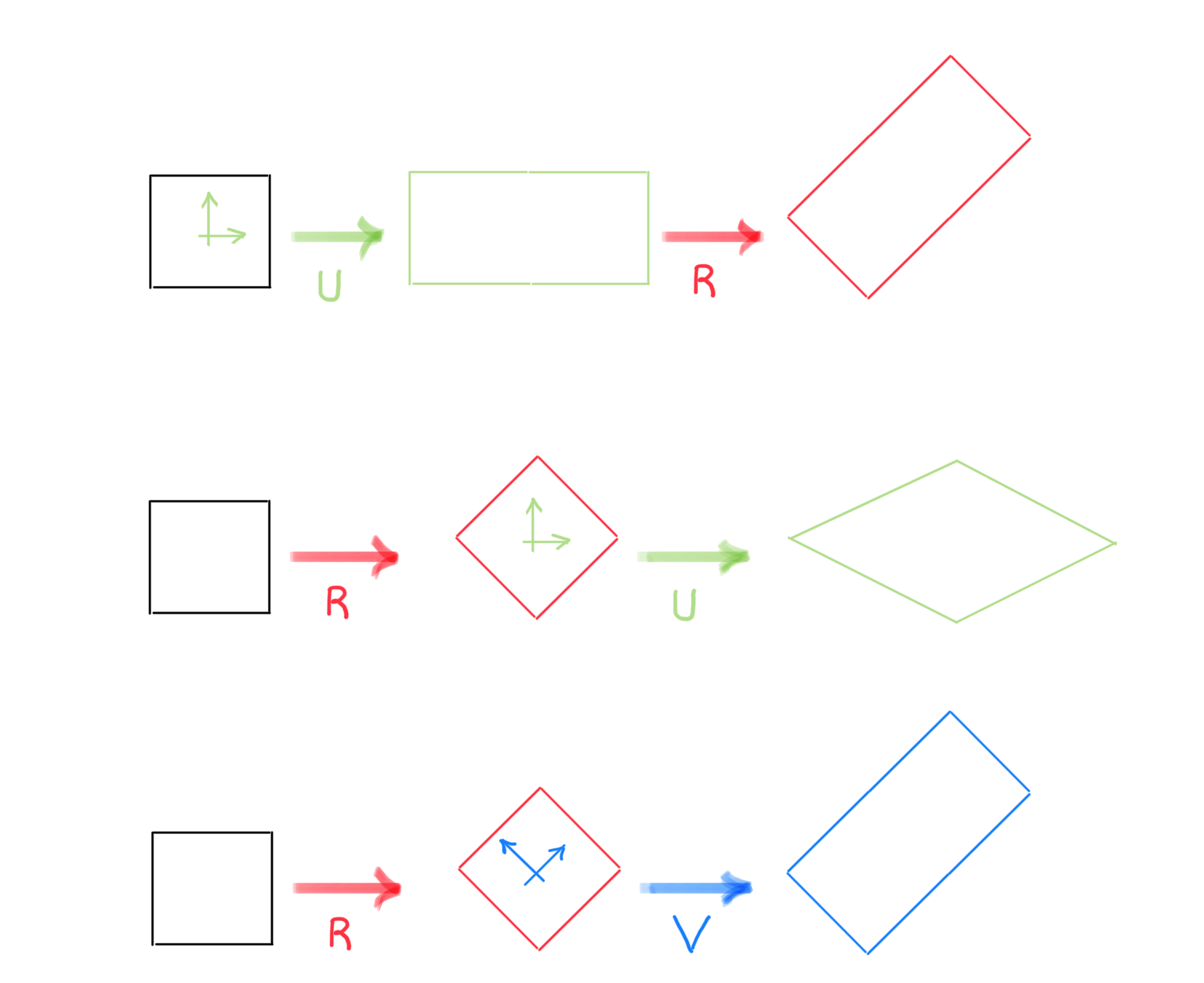
Il teorema di decomposizione polare coglie quindi le trasformazioni elementari, rotazione e deformazione pura, che compongono \(\tens{F}\) e mette in evidenza la non commutatività delle due trasformazioni. Inoltre se \(\tens{R}=\tens{I}\) e quindi \(\tens{F}=\tens{U}=\tens{V}\) la trasformazione, nel punto considerato, è una deformazione pura. Al contrario, \(\tens{U}=\tens{I}=\tens{V}\) e quindi \(\tens{F}=\tens{R}\) la trasformazione, nel punto considerato, è una rotazione rigida.
Osservazione 1.6.3. tensori di rotazione.
Abbiamo già più volte incontrato il tensore 2D relativo ad una rotazione in senso antiorario di \(90^o\) che in termini matriciali ha la seguente espressione
Per tale tensore è facile verificare le seguenti proprietà
Le proprietà elencate non sono specifiche del particolare tensore considerato ma sono soddisfatte da tutti i tensori di rotazione, qualsiasi sia l'entità dell'angolo di rotazione. Al fine di verificare ciò, si consideri la trasformazione lineare che ruota di un generico angolo \(\theta\) un vettore assegnato \(\vec{X}\text{.}\)
Come mostrato nel video si ottiene il seguente risultato
È facile verificare le proprietà
con le quali si definiscono i tensori ortogonali propri. La condizione appena scritta consente di ottenere
relazione che conferma il fatto che il cambio di volume non può che essere legato unicamente alla parte \(\tens{U}\) della trasformazione. È anche facile verificare che
Osservazione 1.6.4. tensori definiti positivi.
Se un tensore simmetrico \(\tens{T}\) verifica la condizione
allora il tensore è definito positivo. Da un punto di vista geometrico tale condizione è facilmente interpretabile come segue: ogni volta che si applica la trasformazione lineare \(\tens{T}\) a qualsiasi vettore non nullo, si ottiene un vettore \(\tens{T}\vec{v}\) che forma con il vettore di partenza \(\vec{v}\) un angolo inferiore a \(\pi/2\text{,}\) condizione che ha comunque, molto spesso, un significato fisico ben preciso.
Sulla condizione di positività verrà fornito un ulteriore approfondimento quando si parlerà di autovalori ed autovettori.
