Solid Mechanics - il tensore della tensione di Cauchy

Paragrafo 2.3 il tensore della tensione di Cauchy

Sottoparagrafo 2.3.1 postulato di Cauchy

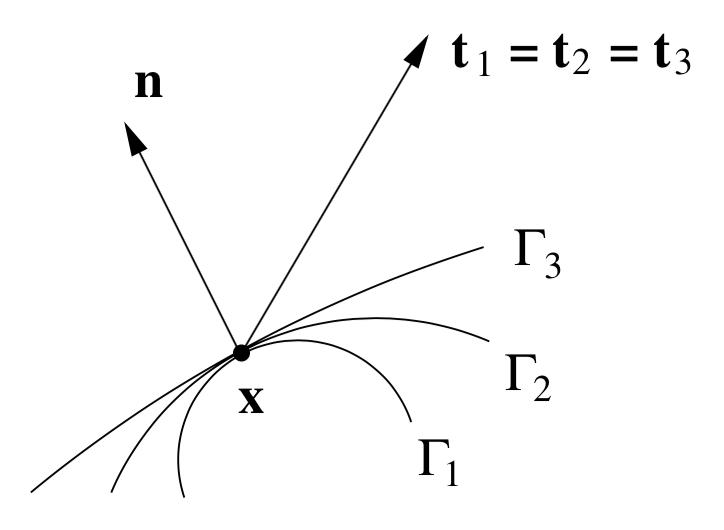
Nella precedente sezione la trazione \(\func{\vec{t}}{\vec{x},\Gamma_{\delta}}\) è stata formulata esplicitando una dipendenza molto generica dalla superficie \(\Gamma_{\delta}\) passante per il punto \(\vec{x}\text{.}\) In base al postulato di Cauchy, fondamentale per tutti gli sviluppi successivi, si assume invece

\begin{equation} \func{\vec{t}}{\vec{x},\Gamma_{\delta}} = \func{\vec{t}}{\vec{x},\vec{n}}\,,\tag{2.3.1} \end{equation}

dove \(\vec{n}\) rappresenta la direzione normale alla superficie individuata da un vettore di lunghezza unitaria. Pertanto viene postulata l'assoluta indipendenza del vettore trazione da fattori come la curvatura della superficie passante per il punto \(\vec{x}\text{.}\) Nella figura vengono mostrate alcune superfici passanti per il punto \(\vec{x}\) e che condividono in tale punto la stessa tangente all superficie e quindi la stessa direzione normale.

Sottoparagrafo 2.3.2 il Teorema della tensione di Cauchy

Si presentano una serie di risultati che presi tutti insieme costituiscono il Teorema della tensione di Cauchy il cui enunciato verrà dato al termine della sezione.

Sotto-sottoparagrafo 2.3.2.1 l'equilibrio sul tetraedro di Cauchy

L'applicazione dell'equazione (2.2.3) assumendo come sottodominio \(\omega\) il tetraedro di Cauchy illustrato nel video precedente fornisce

\begin{equation*} \int_{\omega_{\delta}} \func{\vec{b}}{\vec{x}} \, dv + \int_{\partial\omega_{\delta}} \func{\vec{t}}{\vec{x}, \vec{n}} \, ds = \vec0\,. \end{equation*}

Si è già osservato che quando \(\delta \to 0\) la misura del volume \(\omega_{\delta}\) tende a zero molto più rapidamente della misura della superficie \(\partial\omega_{\delta}\text{.}\) Inoltre \(\partial\omega_{\delta} = \Gamma_{\delta}\cup\Gamma_{1}\cup\Gamma_{2}\cup\Gamma_{3}\text{,}\) allora la precedente equazione diventa

\begin{equation*} \int_{\Gamma_{\delta}} \func{\vec{t}}{\vec{x}, \vec{n}} \, ds + \int_{\Gamma_{1}} \func{\vec{t}}{\vec{x}, -\vec{e}_1} \, ds + \int_{\Gamma_{2}} \func{\vec{t}}{\vec{x}, -\vec{e}_2} \, ds + \int_{\Gamma_{3}} \func{\vec{t}}{\vec{x}, -\vec{e}_3} \, ds = \vec0\,. \end{equation*}

Tenendo conto della relazione geometrica che lega le facce \(\Gamma_{1}\text{,}\) \(\Gamma_{2}\) e \(\Gamma_{3}\) alla faccia \(\Gamma_{\delta}\text{,}\) si ottiene

\begin{equation*} \func{\vec{t}}{\vec{x}, \vec{n}}\,\Gamma_{\delta} + \func{\vec{t}}{\vec{x}, -\vec{e}_1} \,\Gamma_{\delta}\,n_1 + \func{\vec{t}}{\vec{x}, -\vec{e}_2} \,\Gamma_{\delta}\,n_2 + \func{\vec{t}}{\vec{x}, -\vec{e}_3} \,\Gamma_{\delta}\,n_3 = \vec0\,, \end{equation*}

e quindi

\begin{equation} \func{\vec{t}}{\vec{x}, \vec{n}} = - \func{\vec{t}}{\vec{x}, -\vec{e}_1} \,n_1 - \func{\vec{t}}{\vec{x}, -\vec{e}_2} \,n_2 - \func{\vec{t}}{\vec{x}, -\vec{e}_3} \,n_3 \,.\label{cauchy_tetrahedron_eq}\tag{2.3.2} \end{equation}

Sotto-sottoparagrafo 2.3.2.2 principio di azione e reazione

Se nell'equazione (2.3.2) si assume \(\vec{n}=\vec{e}_1\) si ottiene

\begin{equation} \func{\vec{t}}{\vec{x}, \vec{e_1}} = - \func{\vec{t}}{\vec{x}, -\vec{e}_1} \,.\label{cauchy_action_reaction_eq}\tag{2.3.3} \end{equation}

La stessa condizione vale per \(\vec{n}=\vec{e}_2\) e \(\vec{n}=\vec{e}_3\text{.}\)

Sotto-sottoparagrafo 2.3.2.3 il tensore

Sulla base delle equazioni (2.3.2) e (2.3.3) si ottiene

\begin{equation} \func{\vec{t}}{\vec{x}, \vec{n}} =\func{\vec{t}}{\vec{x}, \vec{e}_1} \,n_1 + \func{\vec{t}}{\vec{x}, \vec{e}_2} \,n_2 + \func{\vec{t}}{\vec{x}, \vec{e}_3} \,n_3 \,,\label{cauchy_lt_eq}\tag{2.3.4} \end{equation}

relazione che mostra come la trazione \(\vec{t}\) sia legata alla generica giacitura \(\vec{n}\) mediante una trasformazione lineare, si veda il video sulle trasformazioni lineari in Paragrafo 1.2, rappresentabile attraverso un tensore del secondo ordine. Ovvero

\begin{equation} \func{\vec{t}}{\vec{x}, \vec{n}} =\func{\tens{\sigma}}{\vec{x}}\,\vec{n} \,.\label{cauchy_stress_eq}\tag{2.3.5} \end{equation}

\(\func{\tens{\sigma}}{\vec{x}}\) prende il nome di tensore della tensione di Cauchy.

In forma matriciale la precedente relazione si scrive

\begin{equation} \left[\begin{array}{c}t_1\\t_2\\t_3\end{array}\right] = \left[\begin{array}{ccc} \sigma_{11} \amp \sigma_{12} \amp \sigma_{13} \\ \sigma_{21} \amp \sigma_{22} \amp \sigma_{23} \\ \sigma_{31} \amp \sigma_{32} \amp \sigma_{33} \end{array}\right] \left[\begin{array}{c}n_1\\n_2\\n_3\end{array}\right]\,,\label{cauchy_mat_stress_eq}\tag{2.3.6} \end{equation}

dove compaiono in maniera esplicita le 9 componenti del tensore della tensione. Tali componenti possono essere visualizzate come segue,

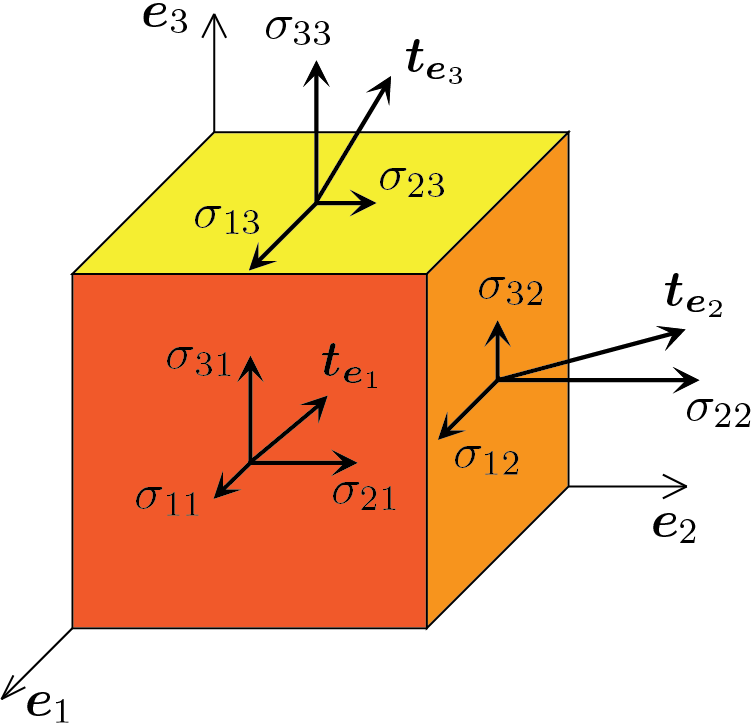
ovvero ciascuna colonna della matrice associata al tensore della tensione

\begin{equation} \mat{\sigma} = \left[\begin{array}{ccc}\vec{t}_{\vec{e}_1} \amp \vec{t}_{\vec{e}_2} \amp \vec{t}_{\vec{e}_3}\end{array}\right]\,,\tag{2.3.7} \end{equation}

contiene le componenti di una delle 3 trazioni agenti sulle giaciture individuate dagli assi coordinati.

Sotto-sottoparagrafo 2.3.2.4 forma differenziale delle equazioni di equilibrio

Si consideri la condizione di annullamento della risultante delle forze applicate, equazione (2.2.3). Tale equazione, grazie alla (2.3.5), può essere riformulata come segue

\begin{equation*} \int_{\omega} \vec{b} \, dv + \int_{\partial\omega} \tens{\sigma}\,\vec{n} \, ds = \vec0\,. \end{equation*}

Per il teorema della divergenza l'integrale di superficie può essere trasformato ottenendo quindi

\begin{equation*} \int_{\omega} \left( \text{div}\tens{\sigma} + \vec{b} \right) \, dv = \vec0\,. \end{equation*}

Tale equazione, per la continuità, deve essere soddisfatta per qualsiasi sottodominio \(\omega\) scelto a piacere del corpo in esame, pertanto si ricava la seguente equazione differenziale

\begin{equation} \text{div}\tens{\sigma} + \vec{b} = \vec0\tag{2.3.8} \end{equation}

da soddisfare in ogni punto del corpo \(\body\text{.}\) Tale equazione vettoriale viene denominata equazione indefinita di equlibrio o, riferendosi alle tre equazioni relative alle singole componenti, equazioni indefinite di equlibrio.

Sotto-sottoparagrafo 2.3.2.5 simmetria del tensore

La condizione di annullamento del momento risultante, equazione (2.2.4), consente di stabilire la simmetria del tensore della tensione. Si tralascia comunque di ricavarla in maniera esplicita e si rimanda ai riferimenti forniti in coda al capitolo.

Teorema 2.3.3 (A.-L. Cauchy).

Dato un corpo soggetto a dei carichi applicati, una condizione necessaria e sufficiente affinché il corpo sia in equilibrio (soddisfacimento delle (2.2.1), (2.2.2)) è che esista un campo tensiorale \(\func{\tens{\sigma}}{\vec{x}}\) tale che

\begin{equation} \func{\vec{t}}{\vec{x}, \vec{n}} =\func{\tens{\sigma}}{\vec{x}}\,\vec{n}\,,\label{T_cauchy_stress_eq}\tag{2.3.9} \end{equation}

\begin{equation} \text{div}\tens{\sigma} + \vec{b} = \vec0\,,\label{T_cauchy_equilibrium_eq}\tag{2.3.10} \end{equation}

\begin{equation} \transp{\tens{\sigma}}=\tens{\sigma}\,.\label{T_cauchy_simmetry_eq}\tag{2.3.11} \end{equation}

Osservazione 2.3.4. osservazioni sulle equazioni indefinite di equilibrio.

Le equazioni (2.3.10) non determinano in maniera completa il campo di tensione di Cauchy per un corpo in equilibrio. In particolare si hanno 3 equazioni differenziali per determinare, per la simmetria del tensore, le \(6\) componenti incognite di \(\tens{\sigma}\text{.}\) Come si vedrà nel seguito tale inconveniente verrà risolto caratterizzando il comportamento costitutivo del materiale di cui è composto il corpo. Comportamento da ricostruire per via sperimentale e riferendosi alla media delle grandezze in gioco. Si ricorda che l'approccio macroscopico non si basa su una precisa descrizione della micro-struttura interna della materia.
Le condizioni al contorno da associare alle equazioni differenziali (2.3.10) saranno determinate mettendo in relazione la tensione incognita \(\tens{\sigma}\) e le trazioni assegnate, \(\bar{\vec{t}}\text{,}\) sul contorno del corpo \(\body\) cui le equazioni di equilibriio si riferiscono. Tale relazione viene stabilita mediante la (2.3.9) che fornisce
\begin{equation} \tens{\sigma}\,\vec{n} = \bar{\vec{t}}\,, \text{su}\;\partial\body\,.\tag{2.3.12} \end{equation}
Tali equazioni costituiscono le condizioni al contorno di tipo naturale per il problema differenziale (2.3.10).
Alla base della derivazione delle equazioni (2.3.10) vi è l'ipotesi di continuità del campo vettoriale \(\vec{b}\) e l'ipotesi di differenziabilità del campo tensoriale \(\tens{\sigma}\text{.}\) Ipotesi che consentono, come visto, di passare da equazioni in forma integrale ad equazioni in forma locale.