Solid Mechanics - analisi dello stato di tensione

Paragrafo 2.4 analisi dello stato di tensione

Sottoparagrafo 2.4.1 convenzione e significato delle componenti del tensore

Riprendiamo la figura già riportata nella sezione precedente per ribadire la convenzione adottata sui segni delle componenti del tensore.

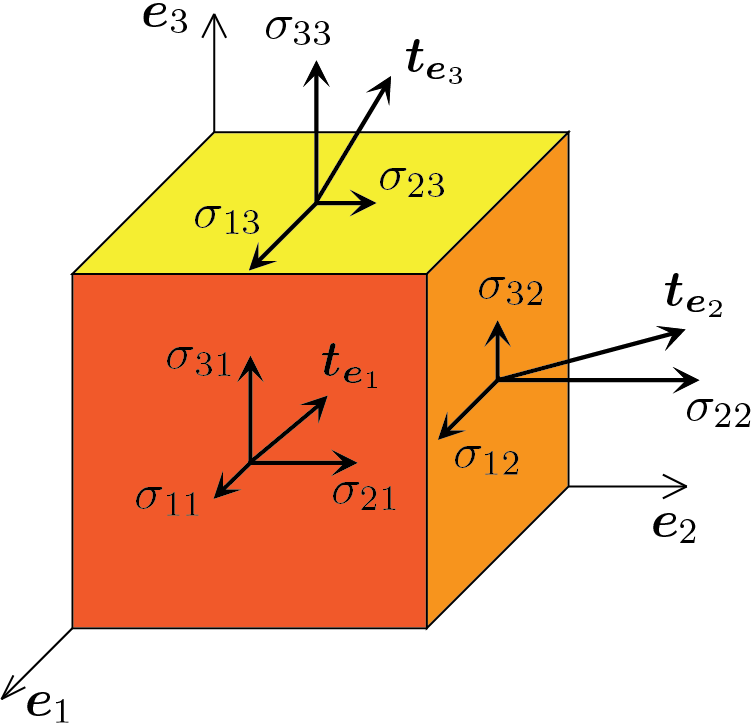
La figura mostra i tre piani che si prendono come riferimento, ovvero i piani aventi come normale uscente gli assi \(\vec{e}_1\text{,}\) \(\vec{e}_2\) e \(\vec{e}_3\text{.}\) A tali facce, che si considerano positive, si riferiscono le componenti del tensore della tensione e la figura riporta tali componenti secondo i versi che si assumono positivi. Se immaginiamo di osservare un cubo, come suggerisce la figura, le facce nascoste del cubo hanno come normale uscente le direzioni opposte \(-\vec{e}_1\text{,}\) \(-\vec{e}_2\) e \(-\vec{e}_3\text{.}\) Su tali facce, che si considerano negative, agiranno le stesse componenti di tensione di segno opposto. Ad esempio sulla faccia avente giacitura \(-\vec{e}_1\) agirà la trazione \(\vec{t}_{-\vec{e}_1} = -\vec{t}_{\vec{e}_1}\text{.}\)

Si consideri la trazione agente sulla giacitura individuata da \(\vec{e}_1\text{,}\) calcolabile anche come

\begin{equation*} \vec{t}_{\vec{e}_1} = \tens{\sigma}\,\vec{e}_1\,. \end{equation*}

Il prodotto scalare fra questa e la giacitura a cui si riferisce fornisce

\begin{equation*} \vec{t}_{\vec{e}_1} \cdot \vec{e}_1 = \sigma_{11} \end{equation*}

che rappresenta, si veda anche la figura, la componente normale della trazione \(\vec{t}_{\vec{e}_1}\text{.}\) Se si calcola il prodotto scalare tra \(\vec{t}_{\vec{e}_1}\) e la direzione \(\vec{e}_2\) si ottiene

\begin{equation*} \vec{t}_{\vec{e}_1} \cdot \vec{e}_2 = \sigma_{21} \end{equation*}

che rappresenta la componente tangenziale della trazione \(\vec{t}_{\vec{e}_1}\) lungo la direzione 2. Analogamente

\begin{equation*} \vec{t}_{\vec{e}_1} \cdot \vec{e}_3 = \sigma_{31} \end{equation*}

rappresenta la componente tangenziale della trazione \(\vec{t}_{\vec{e}_1}\) lungo la direzione 3.

Le stesse valutazioni possono essere fatte per le altre trazioni \(\vec{t}_{\vec{e}_2}\) e \(\vec{t}_{\vec{e}_3}\text{.}\) Quanto si ottiene può essere riepilogato come segue.

Le componenti con indice ripetuto
\begin{equation*} \sigma_{11}\quad\sigma_{22}\quad\sigma_{33} \end{equation*}
costituiscono le componenti normali del tensore. Se il segno è positivo sono componenti di trazione, se è negativo sono componenti di compressione.
Le componenti con indice misto (si ricordi la simmetria)
\begin{equation*} \sigma_{12}\quad\sigma_{13}\quad\sigma_{23} \end{equation*}
costituiscono le componenti tangenziali del tensore. Il segno delle componenti tangenziali segue la convenzione indicata in figura ma, a differenza delle componenti normali, non ha un particolare significato fisico dal momento che il tipo di carico non cambia al cambiare del segno.
Per ogni componente del tensore il secondo indice si riferisce alla giacitura su cui agisce la trazione e il primo indice si riferisce alla componente della trazione.

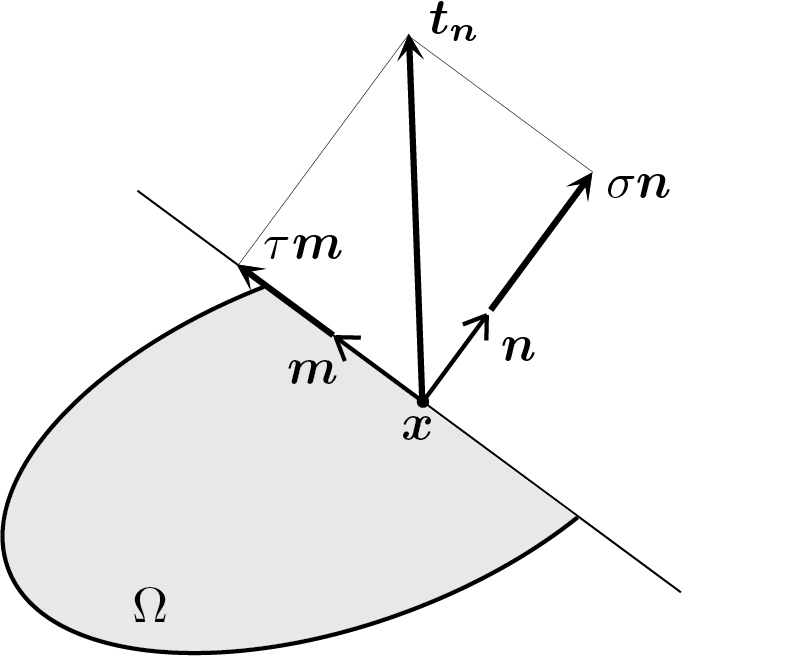
Quanto discusso per le componenti del tensore vale anche per una giacitura generica \(\vec{n}\text{.}\) Come stabilito dal Teorema della tensione di Cauchy si ha

\begin{equation*} \vec{t}_{\vec{n}} = \tens{\sigma}\,\vec{n}\,. \end{equation*}

Da cui si può calcolare la componente normale della trazione

\begin{equation} \sigma = \vec{t}_{\vec{n}} \cdot \vec{n} = \tens{\sigma}\,\vec{n} \cdot \vec{n}\tag{2.4.1} \end{equation}

e la componente tangenziale relativa ad una direzione \(\vec{m}\) ortogonale ad \(\vec{n}\)

\begin{equation} \tau = \vec{t}_{\vec{n}} \cdot \vec{m} = \tens{\sigma}\,\vec{n} \cdot \vec{m} \,.\tag{2.4.2} \end{equation}

Per denotare le due componenti si è utilizzata la convenzione, spesso adottata in ambito ingegneristico, che indica le componenti normale e tangenziale rispettivamente con i simboli \(\sigma\) e \(\tau\text{.}\) Il vettore \(\vec{m}\text{,}\) come \(\vec{n}\text{,}\) è un vettore di lunghezza unitaria.

Sottoparagrafo 2.4.2 tensioni principali e direzioni principali

Quanto discusso nella Paragrafo 1.7 relativa alle direzioni principali del tensore \(\tens{U}\) è applicabile in larga parte anche al tensore della tensione \(\tens{\sigma}\text{.}\) Ambedue i tensori sono simmetrici e l'unico fondamentale distinguo che occorre effettuare è che, a differenza di \(\tens{U}\text{,}\) \(\tens{\sigma}\) non è definito positivo. Pertanto in questo caso gli autovalori, che individuano adesso le tensioni principali del tensore, potranno essere anche nulli o negativi. Comunque la simmetria di \(\tens{\sigma}\) consente la seguente rappresentazione spettrale del tensore

\begin{equation} \tens{\sigma} = \sigma_1\,\vec{s}_1 \otimes \vec{s}_1 + \sigma_2\,\vec{s}_2 \otimes \vec{s}_2 + \sigma_3\,\vec{s}_3 \otimes \vec{s}_3\,,\label{spectral_stress_eq}\tag{2.4.3} \end{equation}

dove le direzioni principali \(\vec{s}_1\text{,}\) \(\vec{s}_2\text{,}\) \(\vec{s}_3\) sono gli autovettori di \(\tens{\sigma}\text{,}\) i quali costituiscono una terna ortonormale, e \(\sigma_1\text{,}\) \(\sigma_2\text{,}\) \(\sigma_3\) sono le tensioni principali.

Nel caso cui le direzioni principali sono allineate con il sistema di riferimento il tensore \(\tens{\sigma}\) assume la semplice forma diagonale

\begin{equation*} \mat{\sigma} = \left[\begin{array}{ccc} \sigma_1 \amp 0 \amp 0 \\ 0 \amp \sigma_2 \amp 0 \\ 0 \amp 0 \amp \sigma_3 \end{array}\right] \end{equation*}

che individua uno stato tensionale descritto solo da componenti di tipo normale. Componenti di trazione se la componente è positiva, di compressione se la componente è negativa. Tale situazione viene illustrata nelle seguente figura.

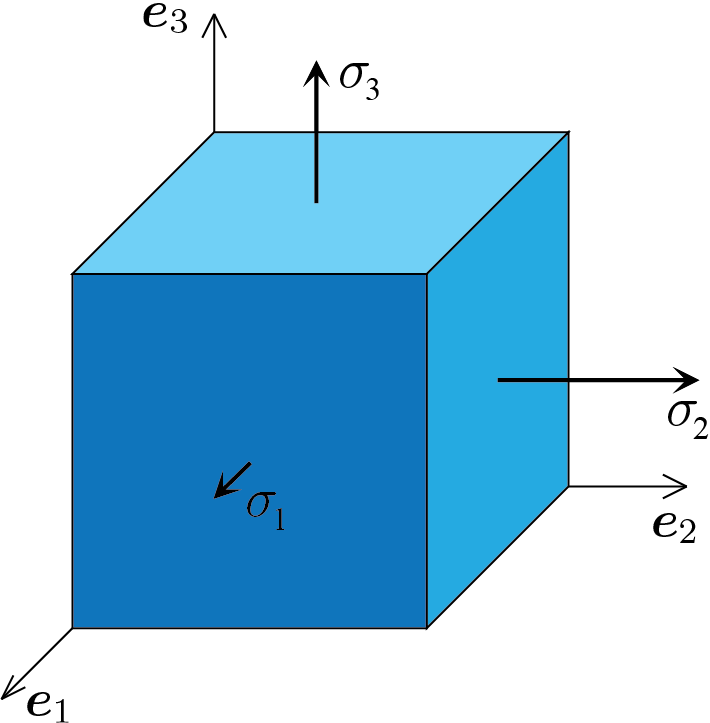
Se invece le direzioni principali non sono allineate con il sistema di riferimento il tensore \(\tens{\sigma}\) assume la forma generica con la presenza anche di componenti tangenziali.

Assegnato un tensore \(\tens{\sigma}\) l'individuazione delle tensioni e delle direzioni principali richiede il calcolo degli autovalori e degli autovettori effetuabile, come si mostrerà in seguito, tramite MATLAB®.

Intuizione 2.4.4. gli invarianti della tensione.

Anche in questo caso, come già discusso nel capitolo dedicato alla cinematica, la soluzione del problema agli autovalori richiede la soluzione di una equazione cubica esprimibile come segue

\begin{equation*} -\sigma^3 + \func{I_1}{\tens{\sigma}} \sigma^2 - \func{I_2}{\tens{\sigma}} \sigma + \func{I_3}{\tens{\sigma}} = 0\,, \end{equation*}

dove compaiono gli invarianti del tensore \(\tens{\sigma}\text{,}\) ovvero le quantità che sono indipendenti dal sistema di riferimento rispetto al quale viene rappresentato \(\tens{\sigma}\text{.}\) Gli invarianti di \(\tens{\sigma}\) sono calcolabili con le seguenti coppie di espressioni, dove ogni coppia contiene la formula da utilizzare nel caso in cui il tensore \(\tens{\sigma}\) sia espresso rispetto alle direzioni principali e la formula da utilizzare nel caso generico.

Primo invariante
\begin{equation} \func{I_1}{\tens{\sigma}} = \sigma_1 + \sigma_2 + \sigma_3 = \trace{\tens{\sigma}}\,,\tag{2.4.4} \end{equation}
dove compare la traccia del tensore ovvero la somma dei coefficienti appartenenti alla diagonale principale.
Secondo invariante
\begin{equation} \func{I_2}{\tens{\sigma}} = \sigma_1\, \sigma_2 + \sigma_2\, \sigma_3 + \sigma_3\, \sigma_1 = \frac{1}{2}\left[(\trace{\tens{\sigma}})^2 - \trace{\tens{\sigma}^2}\right]\,.\tag{2.4.5} \end{equation}
Terzo invariante
\begin{equation} \func{I_3}{\tens{\sigma}} = \sigma_1\, \sigma_2\, \sigma_3 = \det{\tens{\sigma}}\,.\tag{2.4.6} \end{equation}

Sottoparagrafo 2.4.3 stati tensionali di base

Sotto-sottoparagrafo 2.4.3.1 stato sferico o idrostatico

Lo stato tensionale che mantiene sempre la stessa forma rispetto a qualsiasi sistema di riferimento è lo stato caratterizzato da tensioni principali che assumono lo stesso valore, ovvero \(\sigma_1 = \sigma_2 = \sigma_3 = p\text{.}\) In tal caso, utilizzando la (2.4.3), il tensore \(\tens{\sigma}\) assume la seguente forma

\begin{equation*} \tens{\sigma} = p\,\vec{e}_1 \otimes \vec{e}_1 + p\,\vec{e}_2 \otimes \vec{e}_2 + p\,\vec{e}_3 \otimes \vec{e}_3\,, \end{equation*}

ovvero

\begin{equation*} \tens{\sigma} = p \, \tens{I}\,. \end{equation*}

La rappresentazione per componenti fornisce anche

\begin{equation*} \mat{\sigma} = p \left[\begin{array}{ccc} 1 \amp 0 \amp 0 \\ 0 \amp 1 \amp 0 \\ 0 \amp 0 \amp 1 \end{array}\right] = \left[\begin{array}{ccc} p \amp 0 \amp 0 \\ 0 \amp p \amp 0 \\ 0 \amp 0 \amp p \end{array}\right]\,. \end{equation*}

Assumendo \(p\) positivo si ha uno stato di trazione uguale in tutte le direzioni, da qui l'aggettivo sferico. Se invece \(p\) è negativo si ha uno stato di compressione uguale in tutte le direzioni, proprio come avviene per un corpo immerso in un fluido. Da qui l'aggettivo idrostatico.

Sotto-sottoparagrafo 2.4.3.2 stato di trazione o compressione “pura”

Il seguente stato tensionale

\begin{equation*} \tens{\sigma} = \sigma \, \vec{e}_1 \otimes \vec{e}_1\,,\quad \mat{\sigma} = \left[\begin{array}{ccc} \sigma \amp 0 \amp 0 \\ 0 \amp 0 \amp 0 \\ 0 \amp 0 \amp 0 \end{array}\right]\,, \end{equation*}

caratterizzato quindi da tensioni principali pari a \(\sigma_1 = \sigma\text{,}\) \(\sigma_2 = 0\text{,}\) \(\sigma_3 = 0\) e direzioni principali individuate dall'asse \(\vec{e}_1\) e dal piano definito dalgi altri due assi della terna, viene di solito etichettato, in base al segno di \(\sigma\text{,}\) stato di trazione o compressione “pura”.

L'aggetivazione “pura” non deve trarre in inganno in quanto vale solo per la disposizione delle direzioni principali appena descritta. È sufficiente infatti assumere una disposizione differente per le direzioni principali, ad esempio ottenuta con una rotazione generica intorno all'asse \(\vec{e}_3\text{,}\) per avere

\begin{equation*} \tens{\sigma} = \sigma \, \vec{s}_1 \otimes \vec{s}_1\,, \end{equation*}

con

\begin{equation*} \matWp{s}{1} = \left[\begin{array}{c} \cos{\alpha}\\\sin{\alpha}\\0 \end{array}\right]\,. \end{equation*}

Da cui deriva, per il tensore \(\tens{\sigma}\text{,}\) la seguente rappresentazione per componenti

\begin{equation*} \mat{\sigma} = \sigma \left[\begin{array}{ccc} \cos{\alpha}^2 \amp \cos{\alpha}\sin{\alpha} \amp 0 \\ \sin{\alpha}\cos{\alpha} \amp \sin{\alpha}^2 \amp 0 \\ 0 \amp 0 \amp 0 \end{array}\right]\,. \end{equation*}

Costituiscono stati di trazione o compressione “pura” anche i seguenti tensori

\begin{equation*} \tens{\sigma} = \sigma \, \vec{e}_2 \otimes \vec{e}_2\,,\quad \mat{\sigma} = \left[\begin{array}{ccc} 0 \amp 0 \amp 0 \\ 0 \amp \sigma \amp 0 \\ 0 \amp 0 \amp 0 \end{array}\right] \end{equation*}

\begin{equation*} \tens{\sigma} = \sigma \, \vec{e}_3 \otimes \vec{e}_3\,,\quad \mat{\sigma} = \left[\begin{array}{ccc} 0 \amp 0 \amp 0 \\ 0 \amp 0 \amp 0 \\ 0 \amp 0 \amp \sigma \end{array}\right]\,. \end{equation*}

Sotto-sottoparagrafo 2.4.3.3 stato di taglio “puro”

Per la discussione dello stato di taglio “puro” occorre lasciare il punto di vista dato dalle direzioni principali e parlare direttamente di uno stato tensionale caratterizzato dalla seguente rappresentazione per componenti

\begin{equation*} \mat{\sigma} = \left[\begin{array}{ccc} 0 \amp \tau \amp 0 \\ \tau \amp 0 \amp 0 \\ 0 \amp 0 \amp 0 \end{array}\right]\,. \end{equation*}

In tal caso, sempre relativamente al sistema di riferimento \(\vec{e}_1\text{,}\) \(\vec{e}_2\text{,}\) \(\vec{e}_3\) utilizzato, si parlerà di stato di taglio “puro” in quanto l'unica componente non nulla del tensore è \(\sigma_{12}=\sigma_{21}=\tau\text{.}\)

Il calcolo di direzioni principali e tensioni principali mostrerebbe che ci troviamo in un caso differente dai precedenti. Infatti il calcolo degli autovalori ed autovettori, effettuabile con le seguenti istruzioni MATLAB®

syms t;
s = [0 t 0; t 0 0; 0 0 0];
[V, D]=eig(s)

Listato 2.4.8.

fornisce

\begin{equation*} \sigma_1 = \tau\,,\quad\sigma_2 = -\tau\,,\quad\sigma_3 = 0\,, \end{equation*}

\begin{equation*} \matWp{s}{1} = \left[\begin{array}{c} 1/\sqrt{2} \\ 1/\sqrt{2} \\0 \end{array}\right] \,,\quad \matWp{s}{2} = \left[\begin{array}{c} -1/\sqrt{2} \\ 1/\sqrt{2} \\0 \end{array}\right] \,,\quad \matWp{s}{3} = \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right] \,. \end{equation*}

Quindi le direzioni principali sono ruotate di \(\pi/4\) intorno all'asse \(\vec{e}_3\) (si riportano gli autovettori normalizzati anche se, nel caso di calcolo simbolico, MATLAB® non fornisce autovettori normalizzati).

Per quanto discusso, sarebbe stato possibile presentare il caso di taglio “puro”

\begin{equation*} \mat{\sigma} = \left[\begin{array}{ccc} 0 \amp \tau \amp 0 \\ \tau \amp 0 \amp 0 \\ 0 \amp 0 \amp 0 \end{array}\right]\,, \end{equation*}

come lo stato tensionale che si realizza quando il sistema di riferimento è ottenuto ruotando la terna delle direzioni principali di \(\pi/4\) intorno al terzo asse e le tensioni principali sono definite da

\begin{equation*} \sigma_1 = \tau\,,\quad\sigma_2 = -\tau\,,\quad\sigma_3 = 0\,. \end{equation*}

Anche i casi

\begin{equation*} \mat{\sigma} = \left[\begin{array}{ccc} 0 \amp 0 \amp \tau \\ 0 \amp 0 \amp 0 \\ \tau \amp 0 \amp 0 \end{array}\right] \end{equation*}

\begin{equation*} \mat{\sigma} = \left[\begin{array}{ccc} 0 \amp 0 \amp 0 \\ 0 \amp 0 \amp \tau \\ 0 \amp \tau \amp 0 \end{array}\right] \end{equation*}

rappresentano stati di taglio “puro” e anche ad essi, con le dovute precisazioni, si applica tutta la discussione precedente.