Solid Mechanics - motivazione

Paragrafo 3.1 motivazione

Al fine di motivare la necessità di introdurre una modellazione costitutiva nella nostra descrizione del comportamento meccanico dei solidi sotto l'azione dei carichi applicati considereremo un caso di studio semplice (semplice vuol dire solo che le difficoltà analitiche di ricerca di una soluzione statica sono praticamente insesistenti ma la validità di quanto discusso rimane assolutamente generale) e lo analizzeremo utilizzando gli unici strumenti di modellazione al momento a nostra disposizione, ovvero quanto presentato nel Capitolo 1 sulla cinematica dei corpi e nel Capitolo 2 sulla statica corpi.

Sottoparagrafo 3.1.1 analisi statica

Si consideri il seguente corpo con dominio \(\body_0\) delimitato dalle due superfici di estremità \(\Sigma_1\) e \(\Sigma_2\) e dalla superfice \(\Pi\) data dalle altre 4 facce del prisma. Sia \(L\) la lunghezza del prisma avente, lungo l'asse, sezione costante ed individuata dalla generica superficie \(\Sigma\text{.}\) Da un punto di vista geometrico avremo banalmente le seguenti misure di area e di volume

\begin{equation*} \func{A}{\Sigma} = \func{A}{\Sigma_1} = \func{A}{\Sigma_2} = S\,,\qquad \func{V}{\body_0} = L \, \func{A}{\Sigma} = L\, S\,, \end{equation*}

dove per \(S\) si intende l'area della superficie \(\Sigma\) che individua la sezione generica del prisma. I carichi di volume siano nulli, \(\vec{b} = \vec{0}\text{,}\) e si supponga che il prisma sia soggetto alle sole trazioni indicate in figura uguali ed opposte.

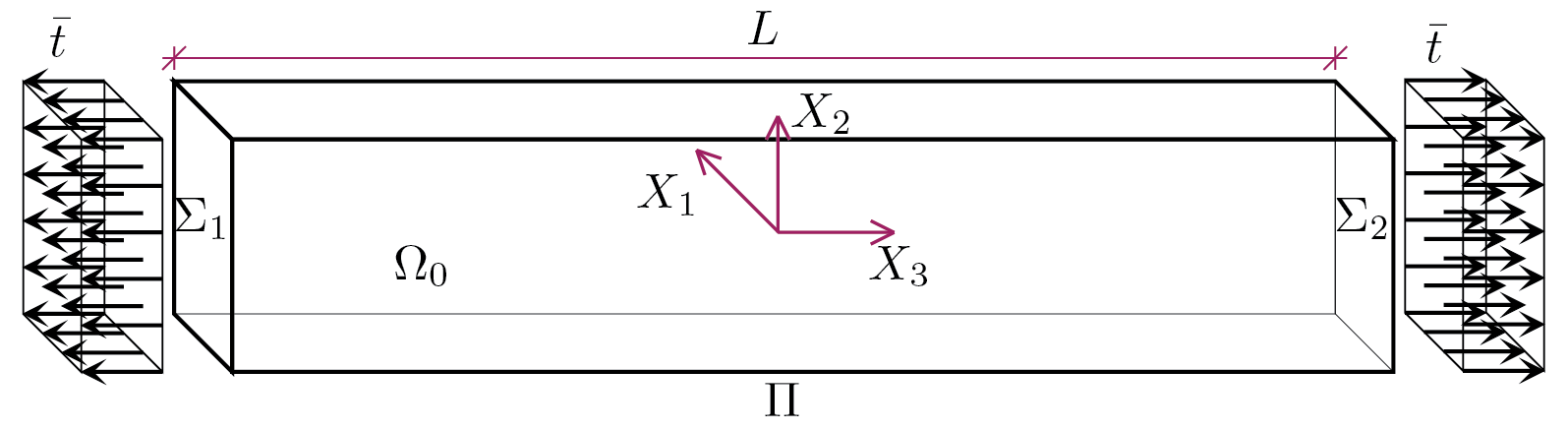
Osservazione 3.1.2. assunzione molto importante.

La descrizione geometrica appena data riguarda solo la configurazione di riferimento \(\body_0\) a cui tipicamente si riferisce la descrizione cinematica dei corpi così come presentato nel Capitolo 1. La scrittura delle equazioni equilibrio, si veda al riguardo il Capitolo 2, viene invece effettuta rispetto alla configurazione corrente \(\body\text{.}\) La seguente discussione quindi dovrebbe tenere conto di tale situazione richiedendo anche l'introduzione di ulteriori concetti che esulano dalla presente trattazione introduttiva di Meccanica dei solidi.

Pertanto si introduce l'ipotesi alla base di una formulazione linearizzata del problema elastico, che è l'obiettivo finale del presente capitolo, ovvero che le equazioni di equilibrio possano essere formulate assumendo

\begin{equation} \body \equiv \body_0 \label{elasticity_basic_assumption_eq}\tag{3.1.1} \end{equation}

vista la piccolezza degli spostamenti e delle deformazioni coinvolte nel problema. Di conseguenza anche tutte le operazioni, ad esempio la derivazione e l'integrazione, saranno svolte rispetto alle coordinate \(X_1\text{,}\) \(X_2\) e \(X_3\) relative alla configurazione di riferimento, o configurazione indeformata, del corpo in esame.

Sulla base dei dati del problema e dell'ipotesi precedente, il problema statico assume la seguente formulazione.

Equazioni indefinite di equilibrio sul dominio
\begin{equation} \text{div}\tens{\sigma} = \vec{0}\quad\;\text{in}\;\body_0\,.\label{motiv_static_eq}\tag{3.1.2} \end{equation}
Ovvero, per componenti, le seguenti tre equazioni scalari
\begin{equation} \begin{array}{l} \frac{\partial\sigma_{11}}{\partial X_1} + \frac{\partial\sigma_{12}}{\partial X_2} + \frac{\partial\sigma_{13}}{\partial X_3} = 0\\ \frac{\partial\sigma_{12}}{\partial X_1} + \frac{\partial\sigma_{22}}{\partial X_2} + \frac{\partial\sigma_{23}}{\partial X_3} = 0\\ \frac{\partial\sigma_{13}}{\partial X_1} + \frac{\partial\sigma_{23}}{\partial X_2} + \frac{\partial\sigma_{33}}{\partial X_3} = 0 \end{array} \quad\;\text{in}\;\body_0\,.\label{motiv_static_components_eq}\tag{3.1.3} \end{equation}
Condizioni, di tipo statico, sul contorno
\begin{align} \amp \tens{\sigma}\vec{n}_1 = \vec{t}_1\quad\;\text{su}\;\Sigma_1 \,,\label{motiv_bc1_eq}\tag{3.1.4}\\ \amp \tens{\sigma}\vec{n}_2 = \vec{t}_2\quad\;\text{su}\;\Sigma_2 \,,\label{motiv_bc2_eq}\tag{3.1.5}\\ \amp \tens{\sigma}\vec{n}_{\Pi} = \vec{0}\quad\;\text{su}\;\Pi \,.\label{motiv_bc3_eq}\tag{3.1.6} \end{align}
Dove
\begin{align} \Sigma_1:\amp \quad \matWp{n}{1} = \left[\begin{array}{r}0\\0\\-1\end{array}\right]\,,\;\matWp{t}{1} = \left[\begin{array}{r}0\\0\\-\bar{t}\end{array}\right] \,,\tag{3.1.7}\\ \Sigma_2:\amp \quad \matWp{n}{2} = \left[\begin{array}{r}0\\0\\1\end{array}\right]\,,\;\matWp{t}{2} = \left[\begin{array}{r}0\\0\\\bar{t}\end{array}\right] \,,\tag{3.1.8}\\ \Pi:\amp \quad \matWp{n}{\Pi} = \left[\begin{array}{r}n_1\\n_2\\0\end{array}\right] \,.\tag{3.1.9} \end{align}

Sotto-sottoparagrafo 3.1.1.1 assunzione sul campo di tensione e soluzione

Nell'equazione (3.1.2) le incognite sono le 6 componenti indipendenti del tensore della tensione mentre le equazioni a disposizione sono soltanto 3. Posta in questi termini la ricerca della soluzione non sarebbe neanche proponibile. Comunque, data la semplicità dei dati del problema si può tentare la strada di assumere una forma per il tensore della tensione e verificare se si riescono a soddisfare tutte le equazioni di equilibrio, indefinite e sul contorno. In particolare si assuma per \(\tens{\sigma}\) la forma seguente

\begin{equation} \mat{\sigma} = \left[\begin{array}{ccc} 0 \amp 0 \amp 0\\ 0 \amp 0 \amp 0\\ 0 \amp 0 \amp \kappa \end{array}\right]\tag{3.1.10} \end{equation}

valida su tutto il dominio e con \(\kappa\) una costante generica. Si verifica facilmente il soddisfacimento delle (3.1.3), infatti

\begin{equation*} \begin{array}{l} \frac{\partial\, 0}{\partial\, X_1} + \frac{\partial\, 0}{\partial\, X_2} + \frac{\partial\, 0}{\partial\, X_3} = 0\\ \frac{\partial\, 0}{\partial\, X_1} + \frac{\partial\, 0}{\partial\, X_2} + \frac{\partial\, 0}{\partial\, X_3} = 0\\ \frac{\partial\, 0}{\partial\, X_1} + \frac{\partial\, 0}{\partial\, X_2} + \frac{\partial\, \kappa}{\partial\, X_3} = 0 \end{array} \quad\;\text{in}\;\body_0\,. \end{equation*}

È verificato anche il soddisfacimento della (3.1.6), infatti

\begin{equation*} \left[\begin{array}{ccc} 0 \amp 0 \amp 0\\ 0 \amp 0 \amp 0\\ 0 \amp 0 \amp \kappa \end{array}\right] \left[\begin{array}{r}n_1\\n_2\\0\end{array}\right] = \left[\begin{array}{r}0\\0\\0\end{array}\right] \,. \end{equation*}

Mentre imponendo la (3.1.4), ugualmente con la (3.1.5), si ottiene

\begin{equation*} \left[\begin{array}{ccc} 0 \amp 0 \amp 0\\ 0 \amp 0 \amp 0\\ 0 \amp 0 \amp \kappa \end{array}\right] \left[\begin{array}{r}0 \\ 0\\-1\end{array}\right] = \left[\begin{array}{r}0\\0\\-\bar{t}\end{array}\right] \quad \rightarrow \quad \kappa = \bar{t} \,. \end{equation*}

In definitiva il campo di tensione che soddisfa tutte le quazioni di equilibrio in gioco è

\begin{equation} \mat{\sigma} = \left[\begin{array}{ccc} 0 \amp 0 \amp 0\\ 0 \amp 0 \amp 0\\ 0 \amp 0 \amp \bar{t} \end{array}\right]\,.\label{motiv_static_solution_eq}\tag{3.1.11} \end{equation}

Quindi la soluzione statica è data da uno stato di trazione pura lungo l'asse \(X_3\) distribuito in maniera omogenea su tutto il corpo.

Sottoparagrafo 3.1.2 analisi cinematica

Sulla base di quanto appreso nel Capitolo 1 e di quanto ottenuto come soluzione statica, siamo in grado di immaginare una trasformazione abbastanza plausibile per il problema in esame. Si consideri ad esempio quanto rappresentato nella seguente figura.

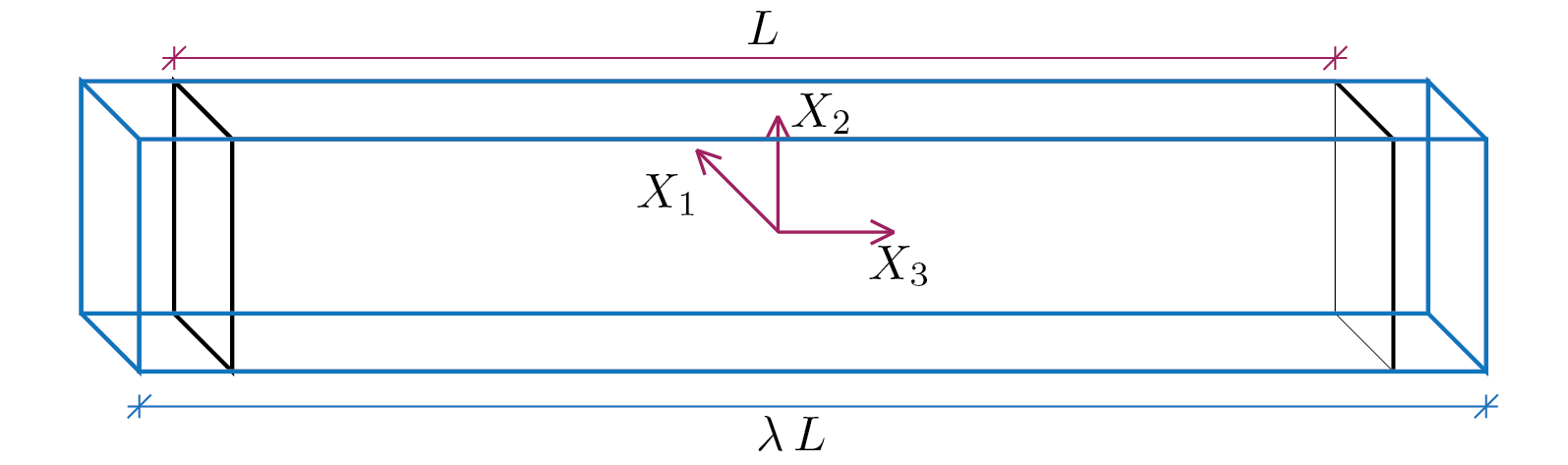
La trasformazione associata è

\begin{align} x_1 \amp = \func{\chi_1}{X_1, X_2, X_3} = X_1\,,\label{motiv_kinematic_solution1_eq}\tag{3.1.12}\\ x_2 \amp = \func{\chi_3}{X_1, X_2, X_3} = X_2\,,\label{motiv_kinematic_solution2_eq}\tag{3.1.13}\\ x_3 \amp = \func{\chi_3}{X_1, X_2, X_3} = \lambda\,X_3\,,\label{motiv_kinematic_solution3_eq}\tag{3.1.14} \end{align}

dove \(\lambda\) è un parametro generico eventualmente da determinare. Il campo di spostamento \(\vec{u}\) ha componenti

\begin{align} u_1 \amp = x_1 - X_1 = 0\,,\label{motiv_displ_solution1_eq}\tag{3.1.15}\\ u_2 \amp = x_2 - X_2 = 0\,,\label{motiv_displ_solution2_eq}\tag{3.1.16}\\ u_3 \amp = x_3 - X_3 = (\lambda - 1)X_3\,,\label{motiv_displ_solution3_eq}\tag{3.1.17} \end{align}

e il gradiente associato è

\begin{equation} \mat{\nabla u} = \left[\begin{array}{ccc} \regulardiff{u_1}{X_1} \amp \regulardiff{u_1}{X_2} \amp \regulardiff{u_1}{X_3}\\ \regulardiff{u_2}{X_1} \amp \regulardiff{u_2}{X_2} \amp \regulardiff{u_2}{X_3}\\ \regulardiff{u_3}{X_1} \amp \regulardiff{u_3}{X_2} \amp \regulardiff{u_3}{X_3} \end{array}\right] = \left[\begin{array}{ccc} 0 \amp 0 \amp 0\\ 0 \amp 0 \amp 0\\ 0 \amp 0 \amp (\lambda - 1) \end{array}\right]\,.\tag{3.1.18} \end{equation}

Per quanto riguarda la descrizione cinematica del problema non siamo in grado di aggiungere altro. Vediamo quindi se utilizzando un altro strumento introdotto nel Capitolo 2, ovvero il Principio dei lavori virtuali, si riesce a ricavare qualche tipo di informazione sul parametro generico \(\lambda\text{.}\)

Sottoparagrafo 3.1.3 Principio dei lavori virtuali

Sulla base del campo di spostamento adottato, i dati del problema in esame e l'assunzione di base (3.1.1), la scrittura del Principio dei lavori virtuali (2.5.5) assume la seguente espressione

\begin{equation} \underbrace{\int_{\Sigma_1} \vec{t}_1 \cdot \vec{u}_1\,dS + \int_{\Sigma_2} \vec{t}_2 \cdot \vec{u}_2\,dS}_{\text{L}_{\text{est}}} = \underbrace{\int_{\body_0} \tens{\sigma} : \text{sym}\tens{\nabla u}\,dV}_{\text{L}_{\text{int}}}\,,\label{motiv_plv_eq}\tag{3.1.19} \end{equation}

dove, nel caso specifico,

\begin{equation*} \matWp{u}{1} = \left[\begin{array}{c}0\\0\\-(\lambda - 1)\frac{L}{2}\end{array}\right]\,,\; \matWp{u}{2} = \left[\begin{array}{c}0\\0\\(\lambda - 1)\frac{L}{2}\end{array}\right]\,,\; \text{sym}\tens{\nabla u} = \tens{\nabla u}\,. \end{equation*}

Introducendo quindi la soluzione statica già trovata e l'espressione sopra riportata del gradiente dello spostamento si ottiene

\begin{equation} \int_{\Sigma_1} \bar{t}\,(\lambda - 1)\frac{L}{2} \,dS + \int_{\Sigma_2} \bar{t}\,(\lambda - 1)\frac{L}{2} \,dS = \int_{\body_0} \bar{t}\,(\lambda - 1) \,dV\,.\tag{3.1.20} \end{equation}

Da cui, svolgendo gli integrali (tutti con argomento costante), si ricava

\begin{equation} \bar{t}\,(\lambda - 1)\frac{L}{2}\,S + \bar{t}\,(\lambda - 1)\frac{L}{2}\,S = \bar{t}\,(\lambda - 1)\,\,S\,L\,,\tag{3.1.21} \end{equation}

ovvero

\begin{equation} \underbrace{\bar{t}\,(\lambda - 1)\,\,L\,S}_{\text{L}_{\text{est}}} = \underbrace{\bar{t}\,(\lambda - 1)\,\,S\,L}_{\text{L}_{\text{int}}}\,,\tag{3.1.22} \end{equation}

Pertanto si riesce anche a verificare l'uguaglianza fra lavoro esterno e lavoro interno ma non traiamo nessuna informazione ulteriore relativamente al parametro \(\lambda\text{.}\)

Sottoparagrafo 3.1.4 considerazioni conclusive

Per quanto discusso sopra, per il problema in esame si possono trarre le seguenti conclusioni.

È stato possibile individuare il tensore \(\sigma\) che soddisfa le equazioni indefinite di equilibrio¹.
Si è individuato un campo di spostamento parametrizzato rispetto al parametro \(\lambda\text{,}\) campo plausibile e che verifica anche il Principio dei lavori virtuali.
Non si riesce, almeno con gli strumenti finora disponibili, a trovare per \(\lambda\) un valore significativo da un punto di vista meccanico. Tale parametro rimane del tutto generico ed indefinito.
Anche la forma assunta per la trasformazione (3.1.12)-(3.1.14) non è stata soggetta a verifica ed al momento rimane del tutto arbitraria.

Tale risultato è stato reso possibile solo dal problema in esame, problema molto particolare che non costituisce quindi la norma. In generale le equazioni di equilibrio non sono risolvibili rispetto alle componenti del tensore delle tesioni.

Il problema messo in evidenza dipende da una mancanza di informazione nel modello meccanico finora presentato. L'informazione mancante è la seguente

Affermazione 3.1.4.

Che legame intercorre fra la deformazione che subisce il corpo e lo stato tensionale che insorge al suo interno?

Nelle sezioni successive viene presentata e discussa tale problematica, non nei termini più generali possibili, ma rispetto al contesto in larga parte già utilizzato per il problema sopra esaminato. Ovvero nel contesto di piccoli spostamenti e piccole deformazioni overro l'ambito degli spostamenti infinitesimi. Pertanto verrà stabilito un legame tra la tensione di Cauchy e il tensore della deformazione infinitesima:

\begin{equation} \tens{\sigma} = \func{\tens{\sigma}}{\tens{\varepsilon}}\,.\tag{3.1.23} \end{equation}

Si ricorda che, per spostamenti infinitesimi, il tensore della deformazione infinitesima costituisce un'approssimazione della deformazione di Green-Lagrange, si veda la Paragrafo 1.9, e che nel calcolo del lavoro interno compare proprio tale tensore. Infatti

\begin{equation} \text{L}_{\text{int}} = \int_{\body_0} \tens{\sigma} : \text{sym}\tens{\nabla u}\,dV = \int_{\body_0} \tens{\sigma} : \tens{\varepsilon}\,dV\,.\tag{3.1.24} \end{equation}