Section 5.3 vincoli
Un corpo o un sistema di corpi tipicamente è soggetto sia ai carichi applicati sia a delle assegnate condizioni di vincolo. Da un punto di vista statico i vincoli vengono trattati rappresentando l’azione esercitata dal vincolo in termini di forze o coppie denominate reazioni vincolari. Tale procedura, come vedremo, consente di ottenere il diagramma di corpo libero mediante il quale il corpo viene rappresentato sotto l’azione di due gruppi di enti statici: le azioni applicate e le reazioni vincolari.
Nel caso piano, in generale, un vincolo applicato può dar luogo a 3 componenti di reazione:
\begin{align*}
H \amp\quad \text{componente orizzontale,}\\
V \amp\quad \text{componente verticale,}\\
\mathcal{M}\amp\quad \text{componente coppia.}
\end{align*}
Dove \(H\) e \(V\) sono le componenti di una forza di reazione, \(\vec{R}\text{,}\) appartenente al piano di lavoro. La presenza, in un punto del corpo, di tutte e 3 le componenti o soltanto di alcune di queste dipende dal tipo di vincolo applicato.
Subsection 5.3.1 assenza di vincolo
È il caso banale in cui in un punto non vi è alcun vincolo applicato, di conseguenza non sarà possibile l’insorgere di componenti di reazione differenti da zero:
\begin{equation}
H=0 \,, \quad V=0 \,,\quad \mathcal{M} = 0\,.\tag{5.3.1}
\end{equation}
Subsection 5.3.2 vincoli semplici
Subsubsection 5.3.2.1 carrello
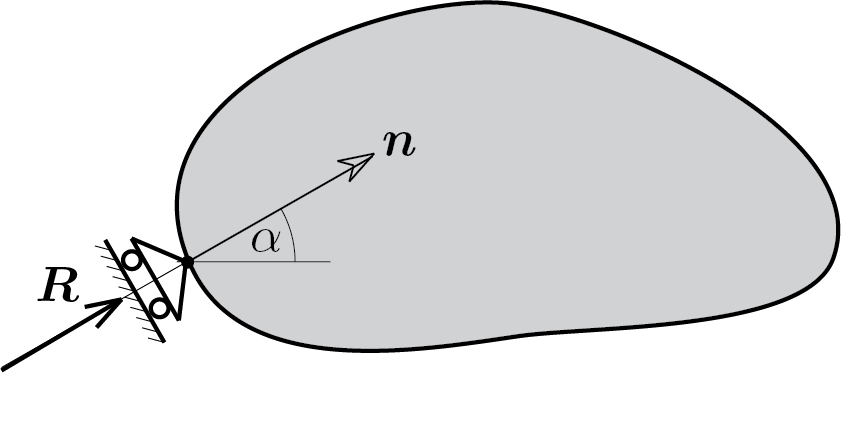
La presenza del carrello determina, dal punto di vista statico, soltanto una forza di reazione, \(\vec{R}\text{,}\) diretta secondo l’asse del carrello. Quindi delle tre componenti di reazione solo le prime due possono essere diverse da zero
\begin{equation}
H \neq 0 \,, \quad V \neq 0 \,,\quad \mathcal{M} = 0\,.\tag{5.3.2}
\end{equation}
Inoltre è nota la direzione della forza di reazione e quindi le due componenti \(H\) e \(V\) non sono fra loro indipendenti ma legate dalla relazione
\begin{equation}
\frac{V}{H} = \tan{\alpha}\,.\tag{5.3.3}
\end{equation}
Ovviamente nel caso cui il carrello abbia asse orizzontale solo \(H\) può essere diversa da zero:
\begin{equation}
H \neq 0 \,, \quad V = 0 \,,\quad \mathcal{M} = 0\,.\tag{5.3.4}
\end{equation}
Nel caso di asse verticale invece
\begin{equation}
H = 0 \,, \quad V \neq 0 \,,\quad \mathcal{M} = 0\,.\tag{5.3.5}
\end{equation}
Subsubsection 5.3.2.2 doppio bipendolo
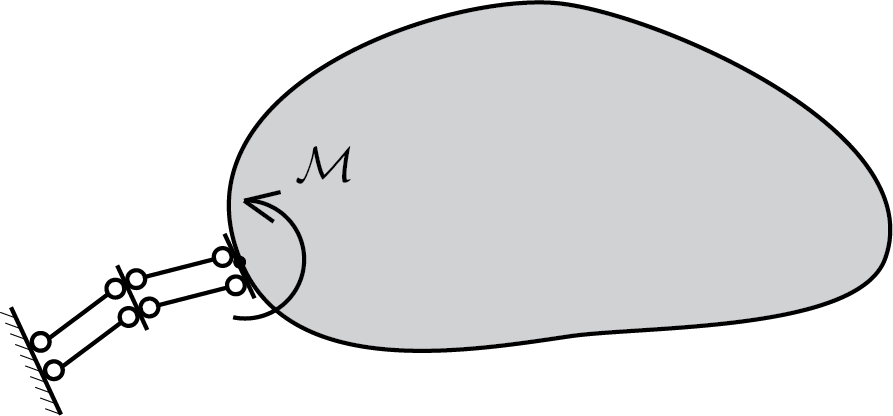
Il doppio bipendolo vincola la rotazione di corpo rigido del corpo rendendo possibile, dal punto di vista statico, solo l’insorgere della componente coppia della reazione vincolare. Pertanto si avrà
\begin{equation}
H = 0 \,, \quad V = 0 \,,\quad \mathcal{M} \neq 0\,.\tag{5.3.6}
\end{equation}
Subsection 5.3.3 vincoli doppi
Subsubsection 5.3.3.1 cerniera
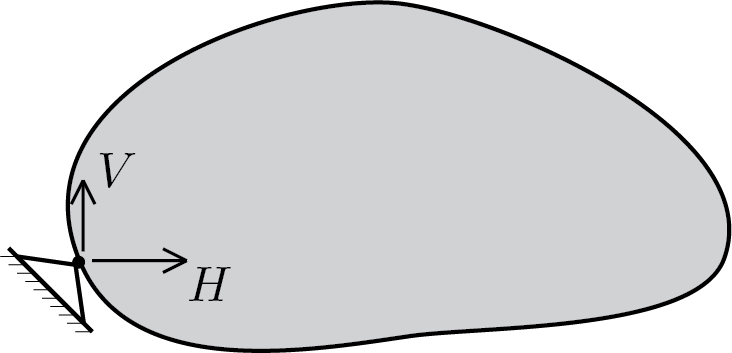
La presenza della cerniera rende possibile, come nel caso del carrello, la presenza di una forza di reazione, \(\vec{R}\text{,}\) la cui direzione non è nota a priori. Pertanto avremo le due componenti di reazione, orizzontale e verticale, eventualmente non nulle e indipendenti
\begin{equation}
H \neq 0 \,, \quad V \neq 0 \,,\quad \mathcal{M} = 0\,.\tag{5.3.7}
\end{equation}
Subsubsection 5.3.3.2 bipendolo
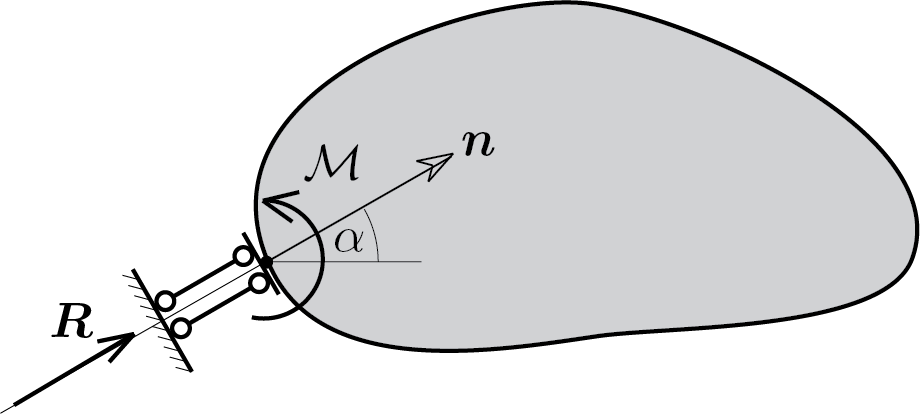
Il bipendolo per le componenti orizzontale e verticale si comporta come il carrello. Il vincolo ulteriore sulla rotazione determina anche la presenza della componte coppia. Pertanto si avrà
\begin{equation}
H \neq 0 \,, \quad V \neq 0 \,,\quad \mathcal{M} \neq 0\,,\tag{5.3.8}
\end{equation}
dove
\begin{equation}
\frac{V}{H} = \tan{\alpha}\,.\tag{5.3.9}
\end{equation}
Anche per il bipendolo se l’asse è orizzontale solo \(H\) può essere diversa da zero:
\begin{equation}
H \neq 0 \,, \quad V = 0 \,,\quad \mathcal{M} \neq 0\,.\tag{5.3.10}
\end{equation}
e nel caso di asse verticale invece
\begin{equation}
H = 0 \,, \quad V \neq 0 \,,\quad \mathcal{M} \neq 0\,.\tag{5.3.11}
\end{equation}
Subsection 5.3.4 vincoli tripli
Subsubsection 5.3.4.1 incastro
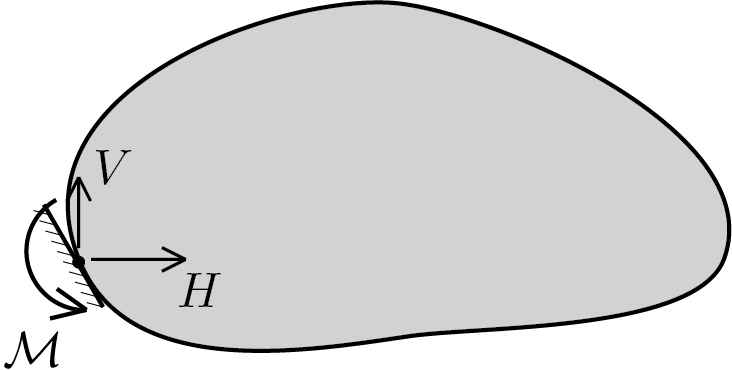
L’incastro determina l’insorgere di una reazione vicolare avente le 3 componenti tutte eventualmente non nulle e indipendenti
\begin{equation}
H \neq 0 \,, \quad V \neq 0 \,,\quad \mathcal{M} \neq 0\,.\tag{5.3.12}
\end{equation}
Subsection 5.3.5 riepilogo
Le figure successive illustrano per il caso piano la rappresentazione grafica dei vincoli e l’eventuale presenza delle componenti di reazione \(H\text{,}\) \(V\) e \(\mathcal{M}\text{.}\)

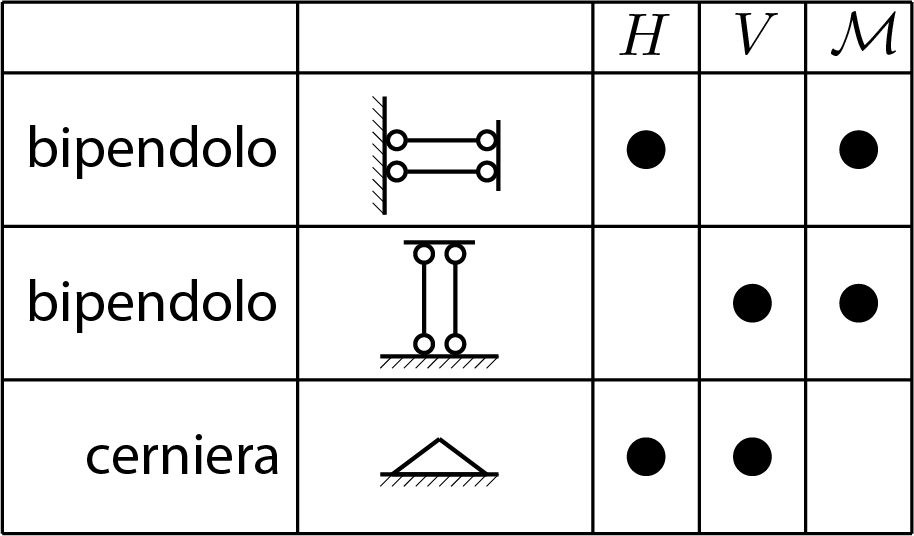
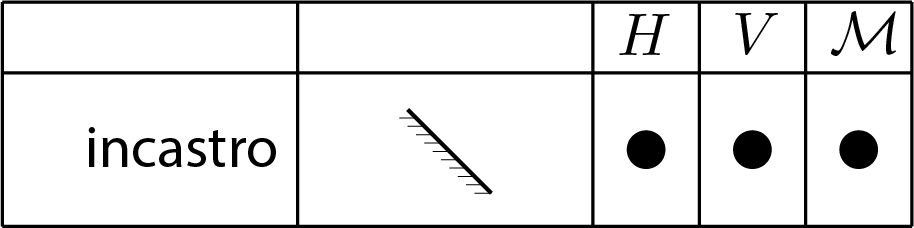
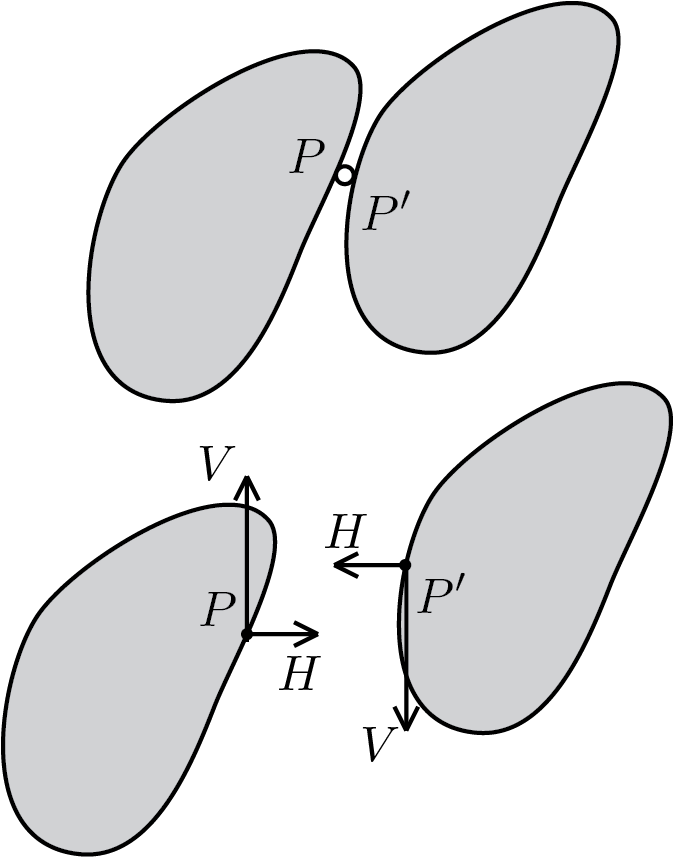
Subsection 5.3.6 vincoli interni
I vincoli interni prescrivono, a differenza dai vincoli esterni, condizioni cinematiche nei punti di contatto tra uno o più corpi. Pertanto, da un punto di vista statico, vengono trattati in termini di reazioni vincolari scambiate dai corpi interessati dalla condizione di vincolo. In figura viene illustrato uno dei casi più ricorrenti, ovvero il caso della cerniera interna.