Section 3.9 esercizi
Subsection 3.9.1
Subsection 3.9.2
In un punto di un foglio sottile di alluminio (\(E = 70\,\left[\text{GPa}\right]\text{,}\) \(\nu = 0.3\)) le uniche componenti non nulle di deformazione sono \(\varepsilon_{11} = 0.001\) e \(\varepsilon_{22} = 0.0005\text{.}\)
Analizzando il problema nel piano \((\vec{e}_1,\vec{e}_2)\) si calcoli quanto segue: tensioni principali e direzioni principali; il tensore della tensione rispetto ad un riferimento inclinato di 30\(^o\) rispetto alle direzioni principali.
Subsection 3.9.3
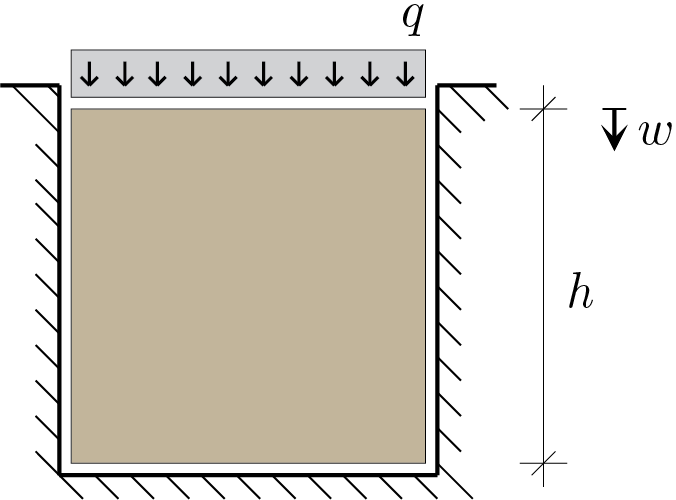
Il pannello elastico mostrato in Figura è costituito da materiale isotropo con parametri costitutivi \(E\) e \(\nu\) generici. La larghezza del pannello coincide esattamente con la larghezza della cavità mentre in direzione verticale il pannello è libero di deformarsi senza che insorgano fenomeni di attrito.
In condizioni piane, si calcoli lo stato tensionale indotto dall’applicazione del carico \(q\) e l’abbassamento in sommità \(w\text{.}\)
Subsection 3.9.4
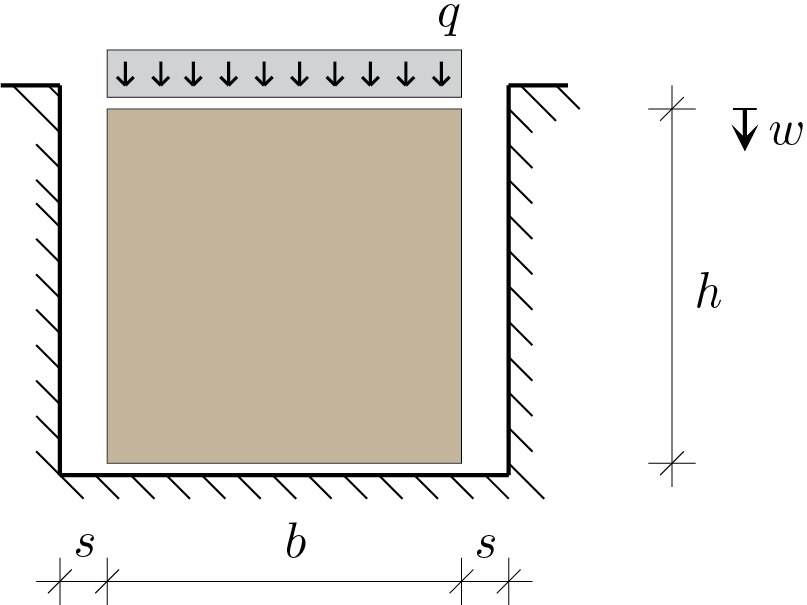
Il pannello elastico mostrato in Figura è costituito da materiale isotropo con parametri costitutivi \(E\) e \(\nu\) generici. Il pannello è appoggiato in una cavità con pareti perfettamente lisce.
In condizioni piane, si calcoli il valore del carico \(q\) in grado di far coincidere la larghezza del pannello \(b\) con la larghezza, \(b+2s\text{,}\) della cavità. Si calcoli anche l’abbassamento in sommità \(w\text{.}\)
Subsection 3.9.5
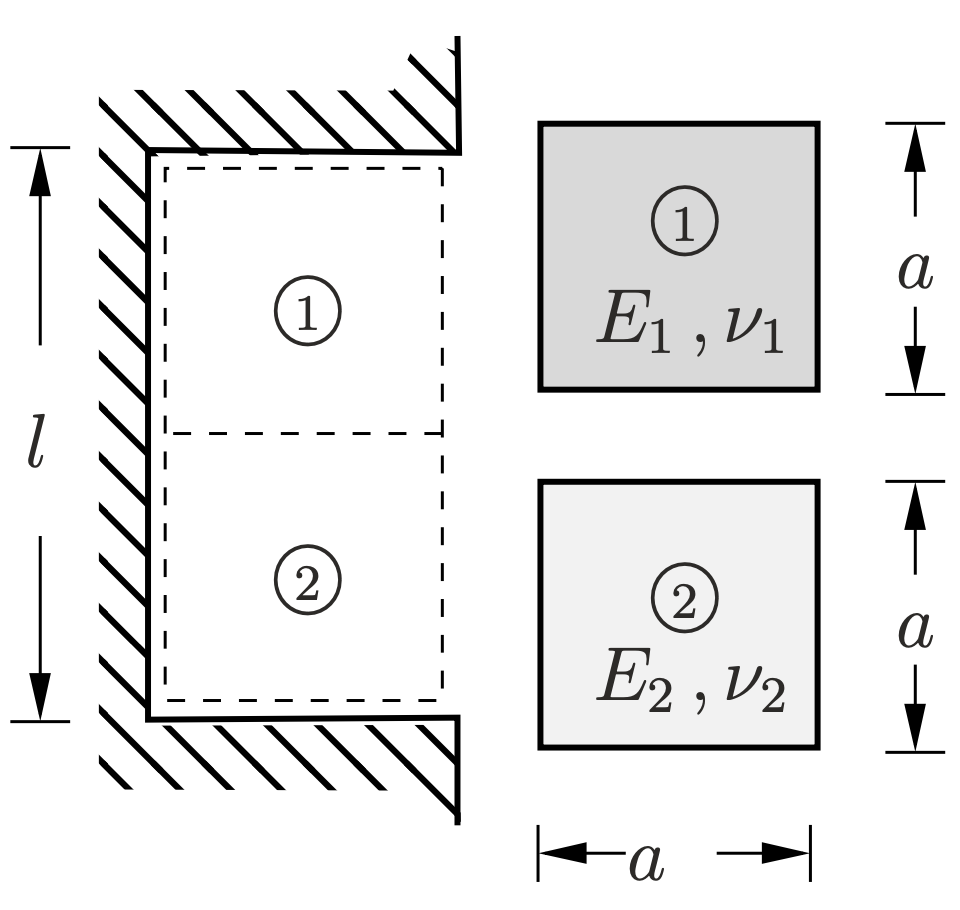
Due pannelli quadrati di materiale differente vengono inseriti nella cavità di altezza \(l\) minore di \(2a\text{.}\) Si risolva il problema elastico assumendo assenti fenomeni di attrito lungo le pareti della cavità.
Subsection 3.9.6
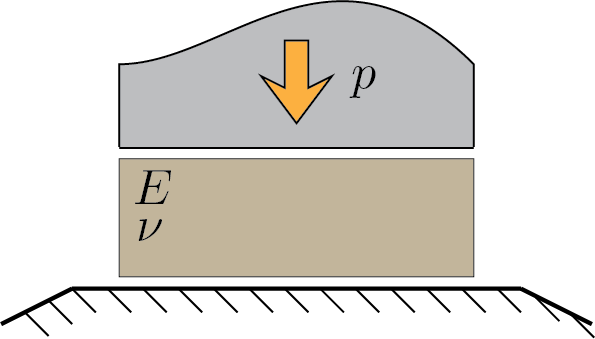
Un blocco di materiale elastico ed isotropo con parametri costitutivi \(E\) e \(\nu\) generici, sia soggetto ad una compressione pari a \(p\) lungo l’asse \(\vec{e}_{3}\text{.}\) Si valutino le componenti di tensione e di deformazione nei seguenti casi:
-
deformazioni impedite lungo le direzioni \(\vec{e}_{1}\) ed \(\vec{e}_{2}\text{;}\)
-
deformazione impedita solo lungo la direzione \(\vec{e}_{1}\text{;}\)
-
deformazioni libere lungo le direzioni \(\vec{e}_{1}\) ed \(\vec{e}_{2}\text{.}\)
Subsection 3.9.7

Si calcoli la soluzione elastica utilizzando il modello di trave tesa. A tal fine si assuma per le caratteristiche della trave modulo di Young pari al valore generico \(E\) e area della sezione pari ad \(A\text{.}\)
A soluzione ottenuta, costruire una rappresentazione grafica dello sforzo normale \(\func{N}{x}\text{.}\)
Subsection 3.9.8
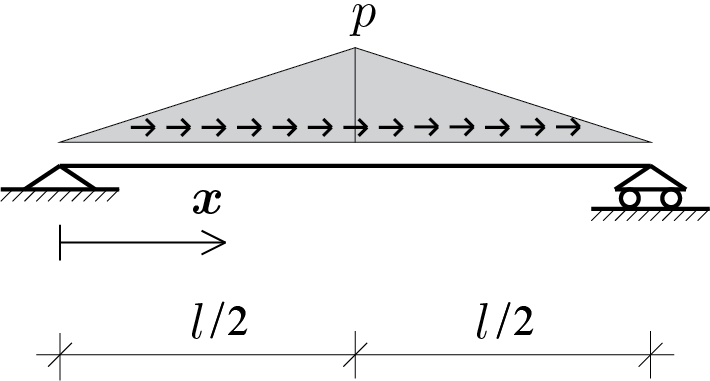
Si calcoli la soluzione elastica utilizzando il modello di trave tesa. A tal fine si assuma per le caratteristiche della trave modulo di Young pari al valore generico \(E\) e area della sezione pari ad \(A\text{.}\)
A soluzione ottenuta, costruire una rappresentazione grafica dello sforzo normale \(\func{N}{x}\text{.}\)
Subsection 3.9.9
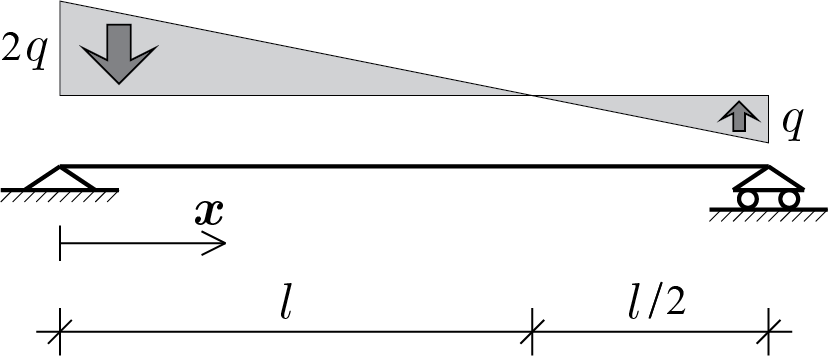
Si calcoli la soluzione elastica utilizzando il modello di trave inflessa. A tal fine si assuma per le caratteristiche della trave modulo di Young pari al valore generico \(E\) e momento d’inerzia della sezione pari ad \(J\text{.}\)
A soluzione ottenuta, costruire una rappresentazione grafica dello spostamento trasversale \(\func{w}{x}\) e del momento flettente \(\func{M}{x}\text{.}\)
Subsection 3.9.10
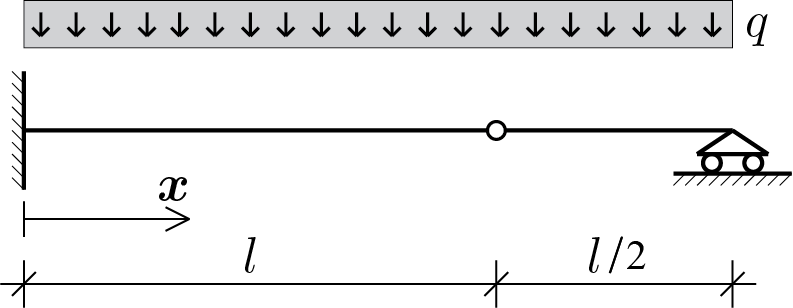
Si calcoli la soluzione elastica utilizzando il modello di trave inflessa. A tal fine si assuma per le caratteristiche della trave modulo di Young pari al valore generico \(E\) e momento d’inerzia della sezione pari ad \(J\text{.}\)
A soluzione ottenuta, costruire una rappresentazione grafica dello spostamento trasversale \(\func{w}{x}\) e del momento flettente \(\func{M}{x}\text{.}\)
