Introduzione alla meccanica dei solidi

Paragrafo 1.3 gradiente della trasformazione

La trasformazione \(\vec{\chi}\) che è stata introdotta per descrivere il moto di un corpo è del tutto generica pertanto non necessariamente è lineare. Ma vedremo come tale caratteristica, la linearità, gioca comunque un ruolo fondamentale perché, anche se generica, \(\vec{\chi}\) viene descritta localmente mediante una sua linearizzazione, linearizzazione che si basa sulla nozione di differenziale di una funzione.

Al fine di richiamare, in maniera semplice, l'idea che sta alla base delle operazioni di linearizzazione, tale processo viene illustrato nello schema seguente per una funzione reale dipendendente da una sola variabile.

\begin{equation*} f \,:\, x \in \mathbb{R} \,\longmapsto\, y \in \mathbb{R} \end{equation*}

\begin{align*} dy \amp = \func{f}{x+dx} - \func{f}{x}\\ \amp = \func{f}{x} +\frac{df}{dx}\,dx + \func{\omega}{dx} - \func{f}{x}\\ \amp =\frac{df}{dx}\,dx + \func{\omega}{dx} \end{align*}

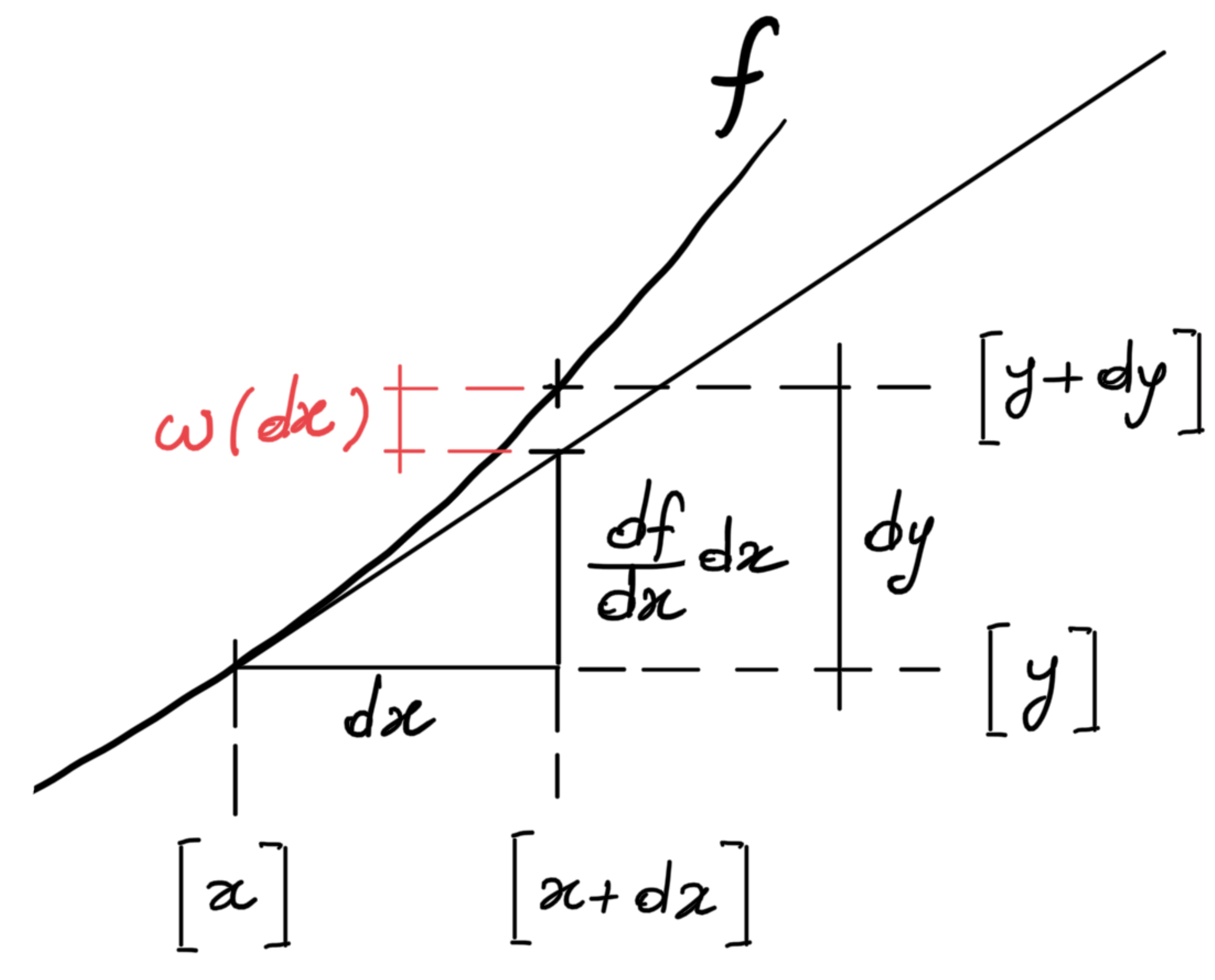
dove \(\func{\omega}{dx}/dx \to 0\) se \(dx \to 0\text{,}\) quindi si può stabilire che

\begin{equation} dy = \frac{df}{dx}\,dx\,.\label{df_eq}\tag{1.3.1} \end{equation}

Una generalizzazione rigorosa dell'equazione (1.3.1) richiederebbe un approfondimento che esula dalle finalità introduttive del presente trattazione. Si riporta quindi direttamente il risultato finale che fornisce il differenziale \(d\vec{x}\) relativo alla configurazione corrente in funzione del differenziale \(d\vec{X}\) relativo alla configurazione di riferimento. A tal fine si premette una scrittura estesa della equazione (1.2.1)

Il differenziale cercato può essere quindi formulato come segue

espressione valutabile anche come prodotto di matrice per vettore, ovvero

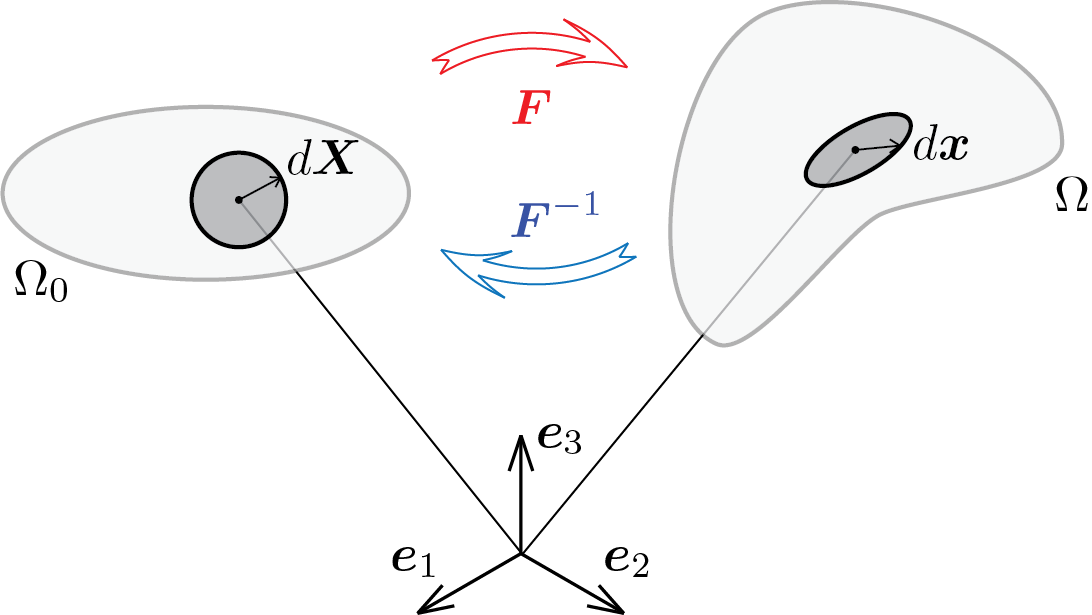
Tale risultato evidenzia come il passaggio da \(d\vec{X}\) a \(d\vec{x}\) avvenga mediante una trasformazione lineare rappresentata dalla matrice \(\mat{F}\) che contiene, punto per punto, tutta l'informazione necessaria per caratterizzare la deformazione. \(\tens{F}\) prende il nome di gradiente della trasformazione con il quale si può esprimere in forma compatta il legame fra i differenziali \(d\vec{X}\) e \(d\vec{x}\)

Relazione che può essere ulteriormente dettagliata come segue

dove è stata esplicitata la dipendenza di \(\tens{F}\) dal punto in cui viene valutato il gradiente.

Quanto ottenuto per la strasformazione \(\vec{\chi}\) vale anche la sua inversa \(\vec{\chi}^{-1}\text{,}\) pertanto si può stabilire il seguente legame inverso fra i differenziali \(d\vec{X}\) e \(d\vec{x}\)

Tipicamente la valutazione del gradiente della trasformazione inversa non passa attraverso la scrittura esplicita di \(\vec{\chi}^{-1}\) ma si effettua calcolando l'inverso di \(\tens{F}\) per il quale deve essere assicurata l'invertibilità.

valutazione del gradiente (trasformazioni non lineari).

Nel caso di trasformazioni non lineari non è possibile identificare una matrice associata alla trasformazione ma, localmente, il gradiente della trasformazione si comporta come una trasformazione lineare. Si consideri, per esempio, la trasformazione così definita

\begin{align*} x_1 \amp = \func{\chi_1}{X_1, X_2} = X_1^3\,,\\ x_2 \amp = \func{\chi_2}{X_1, X_2} = X_2^3\,. \end{align*}

Il calcolo delle derivate parziali

\begin{align*} \regulardiff{\chi_1}{X_1} = 3\,X_1^2\,,\amp\regulardiff{\chi_1}{X_2} = 0\,,\\ \regulardiff{\chi_2}{X_1} = 0\,,\amp\regulardiff{\chi_2}{X_2} = 3\,X_2^2 \end{align*}

consente la valutazione del gradiente della trasformazione

\begin{equation*} \func{\mat{F}}{\vec{X}} = \left[\begin{array}{cc} \regulardiff{\chi_1}{X_1} \amp \regulardiff{\chi_1}{X_2} \\ \regulardiff{\chi_2}{X_1} \amp \regulardiff{\chi_2}{X_2} \end{array}\right] = \left[\begin{array}{cc} 3\,X_1^2 \amp 0 \\ 0 \amp 3\,X_2^2 \end{array}\right] \end{equation*}

Al fine di visualizzare come agisca la trasformazione assegnata si considerano, nel dominio piano \((X_1, X_2)\text{,}\) tre circonferenze di raggio \(0.5\text{,}\) \(1.0\) e \(1.5\) e su queste si applichi la trasformazione non lineare assegnata. Si riportano le istruzioni MATLAB® per il calcolo e il plottaggio delle circonferenze nella configurazione di riferimento e in quella corrente.

N=60;
angle=linspace(0,2*pi,N);

radius=1.0;
c1X=radius*cos(angle);
c1Y=radius*sin(angle);
c1x=c1X.^3;
c1y=c1Y.^3;

radius=0.5;
c2X=radius*cos(angle);
c2Y=radius*sin(angle);
c2x=c2X.^3;
c2y=c2Y.^3;

radius=1.5;
c3X=radius*cos(angle);
c3Y=radius*sin(angle);
c3x=c3X.^3;
c3y=c3Y.^3;

hold on
% circonferenza (r=1) con deformata
plot(c1X,c1Y,'b-')
plot(c1x,c1y,'b-')

% circonferenza (r=0.5) con deformata
plot(c2X,c2Y,'r-')
plot(c2x,c2y,'r-')

% circonferenza (r=1.5) con deformata
plot(c3X,c3Y,'m-')
plot(c3x,c3y,'m-')

Istruzioni che consentono di ottenere la seguente figura dove le tre circonferenze, nelle configurazioni di riferimento e corrente, sono rappresentate con i colori rosso per il raggio \(0.5\text{,}\) blu per il raggio \(1.0\) e magenta per il raggio \(1.5\text{.}\)

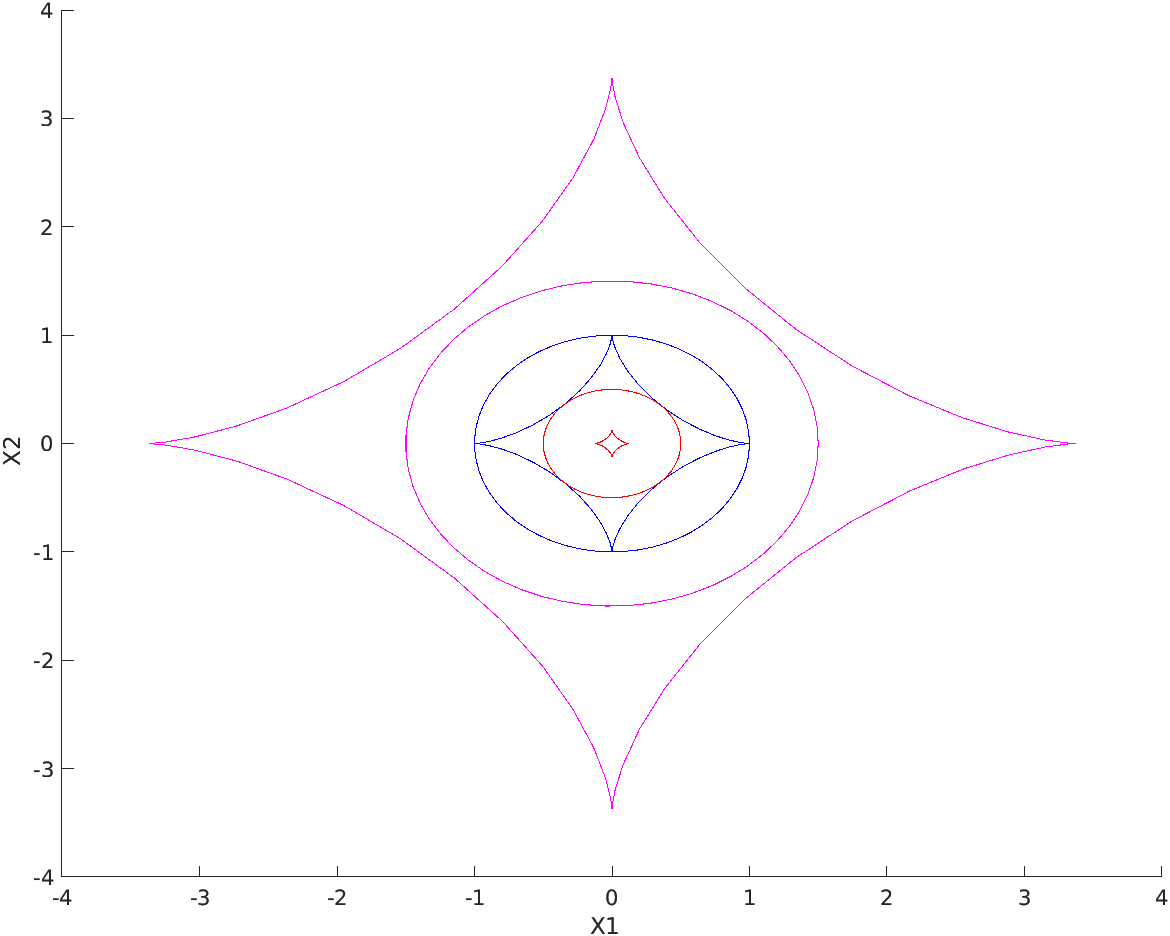
Per esercizio e per confrontare la trasformazione non lineare esaminata con più semplici trasformazioni lineari, si suggerisce di effetuare gli stessi calcoli per le Trasformazioni 2, 3 e 4 discusse nelle sezioni precedenti.